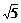(17)(本小题满分12分)
若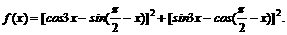
(I)求f (x)的最小正周期;
(II)记g(x)=2f (x)+a 的最小值为-2,求实数a的值.
的最小值为-2,求实数a的值.
(18)(本小题满分12分)
已知圆C的参数方程为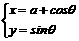 (θ为参数,且θ∈[0, 2π)),且圆C与直线l1: x+y-1=0的两个交点为P、Q,若
(θ为参数,且θ∈[0, 2π)),且圆C与直线l1: x+y-1=0的两个交点为P、Q,若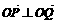 (O为坐标原点).
(O为坐标原点).
(I)求实数a的值;
(II)若a≠0,直线l2与l1有相同的方向向量,且截圆C所得弦长是1,求直线l2的方程.
(19)(本小题满分12分)
甲、乙两个独立地破译一个密码,甲能译出的概率为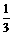 ,乙能译出的概率为x,甲、乙两人中至少有一人能译出的概率为y,恰有一人能译出的概率为
,乙能译出的概率为x,甲、乙两人中至少有一人能译出的概率为y,恰有一人能译出的概率为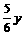 .
.
(I)求x, y的值;
(II)求甲、乙两人都译不出的概率.
(20)(本小题满分12分)
已知函数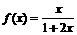 ,数列{an}的首项为
,数列{an}的首项为 ,前n项和为sn,且当n≥2时,sn=f (sn-1).
,前n项和为sn,且当n≥2时,sn=f (sn-1).
(I)证明:数列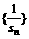 是等差数列,并求出sn的表达式;
是等差数列,并求出sn的表达式;
(II)设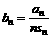 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(21)(本小题满分12分)
已知函数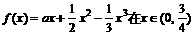 上为增函数.
上为增函数.
(I)求实数a的取值范围;
(II)设f (x)的导函数为f ′(x), g(x)=sinx+cosx-1, a取(1)中的最小值,求证:当x>0时,g(x)>f ′(x).
(22)(本小题满分14分)
已知两点M(-2, 0), N(2, 0),动点P在y轴上的射影是H,若存在常数m使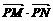 ,m+2, m
,m+2, m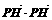 成等差数列.
成等差数列.
(I)求动点P的轨迹C的方程;
(II)当m∈[-4, 0]时,讨论动点P的轨迹是什么图形?
(III)当m=-2时,过点N的直线l交曲线C于x轴下方两个不同点A、B,设R为AB中点,若过点R与点Q(0, -2)的直线交x轴于点D(x0, 0),求x0的取值范围.





(13)二项式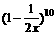 的展开式中含
的展开式中含 的项的系数为_____________.
的项的系数为_____________.
(14)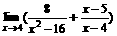 = _____________.
= _____________.
(15)抛物线的顶点是双曲线16x2-9y2=144的中心,焦点是双曲线的左顶点,则该抛物线方
程是_____________.
(16)已知函数f (x)的导函数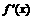 的图像如图所示,给出以下结论:
的图像如图所示,给出以下结论:
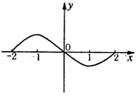 ①函数f (x)在(-2, -1)和(1, 2)上是单调递增函数;
①函数f (x)在(-2, -1)和(1, 2)上是单调递增函数;
②函数f (x)在(-2, 0)上是单调递增函数,在(0, 2)上是单调递减函数;
③函数f (x)在x=-1处取得极大值,在x=1处取得极小值;
④函数f (x)在x=0处取得极大值f (0).
则正确命题的序号是__________(填上所有正确命题的序号)
(1)已知全集U=R,集合A={x|(x+2)(x-1)<0}, B={x|-1≤x<2},则A∩(CU B)为
(A) {x|x<-2, 或x>1} (B) {x|x<-2, 或x≥0}
(C) {x|-2<x<-1} (D) {x|x<-1, 或x>1}
(2)抛物线y2=12x的准线方程为
(A) x=3 (B) x=-3 (C) y=3 (D) y=-3
(3)设向量a=(-1, 2), b=(1, -1), c=(3, -2),若c=λ1a+λ2b,则实数λ1, λ2的值为
(A) λ1=4, λ2=1 (B) λ1=1, λ2=4
(C) λ1=0, λ2=4 (D) λ1=1, λ2=-4
(4)若a>1时,则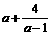 的最小值为
的最小值为
(A) 2 (B) 3 (C) 4 (D) 5
(5)设z=a+bi, 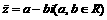 且
且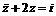 ,则
,则 的值为
的值为
(A) i (B) –i (C) 1-i (D)1+i
(6)在等比数列 中,
中, ,则
,则
(A) (B)
(B)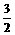 (C)
(C)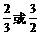 (D)
(D)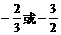
(7)设正态函数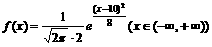 ,则下列命题不正确的是
,则下列命题不正确的是
(A)总体的平均数为10
(B)函数f (x)的曲线是关于直线x=10对称
(C)函数f (x)的曲线与x轴有交点
(D)总体的标准差为2
(8)已知变量x、y满足下列条件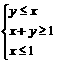 ,则目标函数z=2x+y的最小值为
,则目标函数z=2x+y的最小值为
(A) 3 (B)
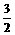 (C)
2 (D)
(C)
2 (D)
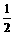
(9)若sin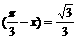 则cos
则cos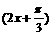 =
=
(A) 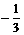 (B)
(B)
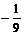 (C)
(C)
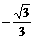 (D)
(D)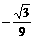
(10)已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若∆ABF2是正三角形,则这个椭圆的离心率是
(A)  (B)
(B)
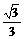 (C)
(C)
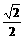 (D)
(D)
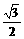
(11)称集合A的非空真子集的真子集叫做集合A的“孙子集”,则集合A={a, b, c, d, e}的孙子集共有
(A) 11个 (B) 39个 (C) 26个 (D) 10个
(12)设函数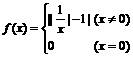 ,则关于x的方程f 2(x)+bf
(x)+c=0有7个不同实数解的充要条件是
,则关于x的方程f 2(x)+bf
(x)+c=0有7个不同实数解的充要条件是
(A) -1<b<0且c>0 (B)b>0且c>0
(C) -1<b<0且c=0 (B)b≥0且c=0
泸州市高中2006级第二次教学质量诊断性考试
数 学(理工农医类)
第II卷(非选择题 共90分)
19. 湖北省部分重点中学2005年春季期中联考
湖北省部分重点中学2005年春季期中联考
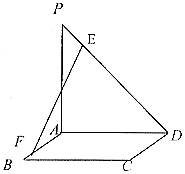
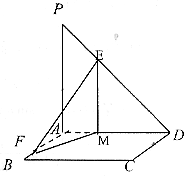
如图,ABCD是矩形,PA⊥平面ABCD,
PA=AD=a,AB=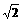 a,E是线段PD上的点,F是线段AB
a,E是线段PD上的点,F是线段AB
上的点,且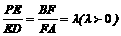 .
.
(I)当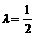 时,求直线EF与平面ABCD所成角的正弦值:
时,求直线EF与平面ABCD所成角的正弦值:
(Ⅱ)是否存在实数λ,使异面直线EF与CD所成角为
60°?若存在,试求出λ的值;若不存在,请说明
 理由.
理由.
5.(1)∵AB⊥平面BCD, ∴AB⊥CD,∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC. 3分
又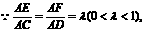 ∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF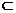 平面BEF,
平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC. 6分
(2)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC. 8分 ∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴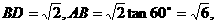 10分
10分
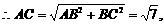 由AB2=AE·AC 得
由AB2=AE·AC 得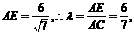
故当 时,平面BEF⊥平面ACD. 12分
时,平面BEF⊥平面ACD. 12分
5.[2005年高考重庆地区信息试卷数学试题]
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且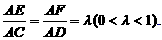
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
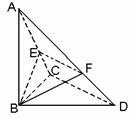 (Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
4.[北 京 四 中2005年数学第一次统测(理科)]
如图,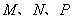 分别是正方体的棱
分别是正方体的棱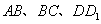 上的点.
(1)若
上的点.
(1)若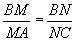 ,求证:无论点
,求证:无论点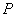 在
在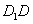 上如何移动,总有
上如何移动,总有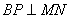 ;
(2)若
;
(2)若 ,且
,且 平面
平面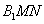 ,求二面角
,求二面角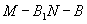 的大小.
的大小.
 4.(I)证法一:连AC、BD,则BD⊥AC,
∵
4.(I)证法一:连AC、BD,则BD⊥AC,
∵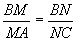 , ∴MN//AC,∴BD⊥MN.
又∵DD1⊥平面ABCD,∴DD1⊥MN,
∴MN⊥平面BDD1.
∵无论点P在DD1上如何移动,总有BP
, ∴MN//AC,∴BD⊥MN.
又∵DD1⊥平面ABCD,∴DD1⊥MN,
∴MN⊥平面BDD1.
∵无论点P在DD1上如何移动,总有BP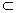 平面BDD1,
故总有MN⊥BP.
证法二:连结AC、BD,则AC⊥BD.
∵
平面BDD1,
故总有MN⊥BP.
证法二:连结AC、BD,则AC⊥BD.
∵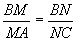 , ∴MN//AC,∴ MN⊥BD,又PD⊥平面ABCD,
由三垂线定理得:MN⊥PB.
(II)解法一:过P作PG⊥C1C交CC1于G,连BG交B1N于O1,
∵PB⊥平面B1MN, ∴PB⊥B1N.
又∵PG⊥平面B1BCC1, ∴ BG⊥B1N,∴ΔBB1N≌ΔBCG,
∴ BN=CG,NC=GC1,
∴BN∶NC=DP∶PD1=2∶1.
同理BM∶MA=DP∶PD1=2∶1.
设AB=3a, 则BN=2a, ∴
, ∴MN//AC,∴ MN⊥BD,又PD⊥平面ABCD,
由三垂线定理得:MN⊥PB.
(II)解法一:过P作PG⊥C1C交CC1于G,连BG交B1N于O1,
∵PB⊥平面B1MN, ∴PB⊥B1N.
又∵PG⊥平面B1BCC1, ∴ BG⊥B1N,∴ΔBB1N≌ΔBCG,
∴ BN=CG,NC=GC1,
∴BN∶NC=DP∶PD1=2∶1.
同理BM∶MA=DP∶PD1=2∶1.
设AB=3a, 则BN=2a, ∴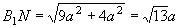 ,
,
 ,
连MO1,∵AB⊥平面B1BCC1, ∴ MO1⊥B1N,
∵∠MO1B就是二面角M-B1N-B的平面角,
,
连MO1,∵AB⊥平面B1BCC1, ∴ MO1⊥B1N,
∵∠MO1B就是二面角M-B1N-B的平面角,
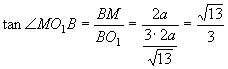 ,∴
,∴  .
解法二:设BD与MN相交于F,连结B1F,
∵PB⊥平面MNB1, ∴ PB⊥B1F,PB⊥MN,
∴在对角面BB1D1D内,ΔPBD∽ΔBB1F,
设BB1=DD1=3,则PD=2,
.
解法二:设BD与MN相交于F,连结B1F,
∵PB⊥平面MNB1, ∴ PB⊥B1F,PB⊥MN,
∴在对角面BB1D1D内,ΔPBD∽ΔBB1F,
设BB1=DD1=3,则PD=2,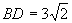 ,∴
,∴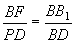 , 即
, 即 ,故
,故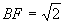 .
∵MN⊥PB,由三垂线定理得MN⊥BD,MN//AC,MN=2BF=
.
∵MN⊥PB,由三垂线定理得MN⊥BD,MN//AC,MN=2BF=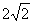 , BN=2,
, BN=2,
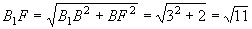 .
设二面角B-B1N-M的平面角为α,则
.
设二面角B-B1N-M的平面角为α,则 ,
,
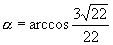 .
.
3.解:(1)当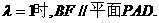 (1分)
(1分)
证明:取PD中点E,则EF//CD,且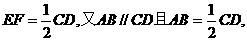
∴四边形ABFE为平行四边形. (3分)
∴BF//AE. 又AE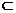 平面PAD ∴BF//平面PAD (4分)
平面PAD ∴BF//平面PAD (4分)
(2) 平面ABCD,
平面ABCD,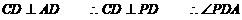 即是二面角的平
即是二面角的平
面角 (5分)
(5分)
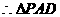 为等腰直角三角形,
为等腰直角三角形,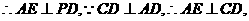
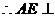 平面PCD 又BF//AE,
平面PCD 又BF//AE,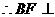 平面PCD.
平面PCD. 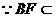 平面PBC,
平面PBC,
∴平面PCD⊥平面PBC,即二面角B-PC-D的大小为90°. (8分)
(3)在平面PCD内作EH⊥PC于点H,由平面PCD⊥平面PBC且平面PCD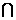
平面PBC=PC知:EH⊥平面PBC. (9分)
在 ,
,
在 代入得:
代入得:
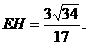 即点E到平面PBC的距离为
即点E到平面PBC的距离为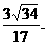 (11分)
(11分)
又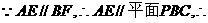 点A到平面PBC的距离为
点A到平面PBC的距离为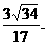 (12分)
(12分)
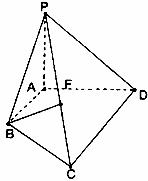
3.[哈尔滨三中东北育才大连育明 天津耀华2005年四校高考模拟联考]
如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=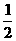 CD.
CD.
(I)点F在线段PC上运动,且设 为何值时,BF//平面PAD?并证明你的结论;
为何值时,BF//平面PAD?并证明你的结论;
(Ⅱ)二面角F-CD-B为45°,求二面角B-PC-D的大小;
(Ⅲ)在(Ⅱ)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.