24.(案中)给出下列四个命题:
(1) 各侧面都是正方形的棱柱一定是正棱柱
(2) 若一个简单多面体的各顶点都有三条棱,则其顶点数V,面数F满足的关系式为2F-V=4
(3) 若直线L⊥平面α,L∥平面β,则α⊥β
(4) 命题“异面直线a,b不垂直,则过a的任一平面和b都不垂直”的否定,其中,正确的命题是 ( )
A、(2)(3) B、(1)(4) C、(1)(2)(3) D、(2)(3)(4)
正确答案:(A)
错误原因:易认为命题(1)正确
二填空题:
23.(案中)底面是正三角形,且每个侧面是等腰三角形的三棱锥是
A、一定是正三棱锥 B、一定是正四面体 C、不是斜三棱锥 D、可能是斜三棱锥
正确答案:(D)
错误原因:此是正三棱锥的性质,但很多学生凭感觉认为如果侧面是等腰三角形,则侧棱长相等,所以一定是正三棱锥,事实上,只须考察一个正三角形绕其一边抬起后所构成的三棱锥就知道应选D
22.(薛中)空间四边形中,互相垂直的边最多有( )
A、1对 B、2对 C、3对 D、4对
答案:C
错解:D
错因:误将空间四边形理解成四面体,对“空间四边形”理解不深刻。
21.(薛中)如果a,b是异面直线,P是不在a,b上的任意一点,下列四个结论:(1)过P一定可作直线L与a , b都相交;(2)过P一定可作直线L与a , b都垂直;(3)过P一定可作平面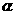 与a , b都平行;(4)过P一定可作直线L与a , b都平行,其中正确的结论有( )
与a , b都平行;(4)过P一定可作直线L与a , b都平行,其中正确的结论有( )
A、0个 B、1个 C、2个 D、3个
答案:B
错解:C 认为(1)(3)对
D 认为(1)(2)(3)对
错因:认为(2)错误的同学,对空间两条直线垂直理解不深刻,认为作的直线应该与a,b 都垂直相交;而认为(1)(3)对的同学,是因为设能借助于两个平行平面衬托从而对问题的分析欠严密。
20.(丁中)若平面 外的直线
外的直线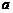 与平面
与平面 所成的角为
所成的角为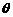 ,则
,则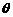 的取值范围是 ( )
的取值范围是 ( )
(A)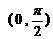 (B)
(B)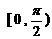 (C)
(C)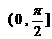 (D)
(D)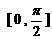
错解:C
错因:直线在平面 外应包括直线与平面平行的情况,此时直线
外应包括直线与平面平行的情况,此时直线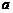 与平面
与平面 所成的角为0
所成的角为0
正解:D
19.(江安中学)
|
|
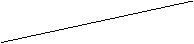 已知AB是异面直线的公垂线段,AB=2,且
已知AB是异面直线的公垂线段,AB=2,且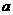 与
与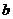 成
成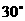 角,在直线
角,在直线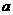 上取AP=4,则点P到直线
上取AP=4,则点P到直线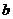 的距离是(
)。
的距离是(
)。
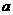
E.
|

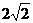
F. 4
G.
|

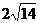
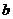
H.
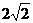 或
或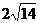
正解:A。过B作BB’∥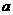 ,在BB’上截取BP’=AP,连结PP’,过P’作P’Q
,在BB’上截取BP’=AP,连结PP’,过P’作P’Q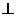
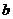 连结PQ,
连结PQ, PP’
PP’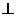 由BB’和
由BB’和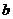 所确定的平面,
所确定的平面, PP’
PP’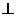
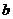
 PQ即为所求。在Rt
PQ即为所求。在Rt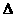 PQP’中,PP’=AB=2,P’Q=BP’,
PQP’中,PP’=AB=2,P’Q=BP’, =AP
=AP
 =2,
=2,  PQ=
PQ=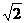 。
。
误解:D。认为点P可以在点A的两侧。本题应是由图解题。
18.(江安中学)球的半径是R,距球心4R处有一光源,光源能照到的地方用平面去截取,则截面的最大面积是( )。
A. 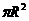
B.
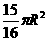
C.
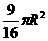
D. 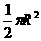
 正解:B。
正解:B。
如图,在 中,
中,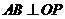 于
于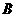
则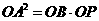 即
即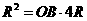
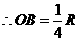 又
又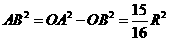
 以
以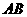 为半径的圆的面积为
为半径的圆的面积为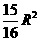
误解:审题不清,不求截面积,而求球冠面积。
17.(江安中学)一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D、E、F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的( )
A.
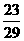
B.
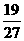
C.
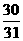
D.
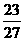
正解:D。
当平面EFD处于水平位置时,容器盛水最多

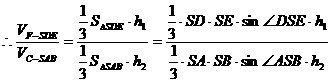

最多可盛原来水得1-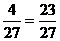
误解:A、B、C。由过D或E作面ABC得平行面,所截体计算而得。
16.(江安中学)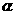 和
和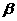 是两个不重合的平面,在下列条件中可判定平面
是两个不重合的平面,在下列条件中可判定平面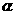 和
和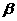 平行的是(
)。
平行的是(
)。
A.
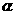 和
和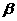 都垂直于平面
都垂直于平面
B.
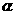 内不共线的三点到
内不共线的三点到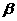 的距离相等
的距离相等
C.
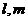 是
是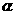 平面内的直线且
平面内的直线且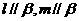
D.
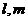 是两条异面直线且
是两条异面直线且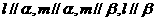
正解:D
对于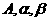 可平行也可相交;对于B三个点可在
可平行也可相交;对于B三个点可在 平面同侧或异侧;对于
平面同侧或异侧;对于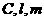 在平面
在平面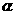 内可平行,可相交。
内可平行,可相交。
对于D正确证明如下:过直线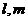 分别作平面与平面
分别作平面与平面 相交,设交线分别为
相交,设交线分别为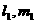 与
与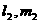 ,由已知
,由已知 得
得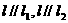 ,从而
,从而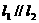 ,则
,则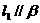 ,同理
,同理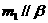 ,
,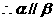 。
。
误解:B
往往只考虑距离相等,不考虑两侧。
15.(江安中学)设a,b,c表示三条直线, 表示两个平面,则下列命题中逆命题不成立的是(
)。
表示两个平面,则下列命题中逆命题不成立的是(
)。
A.
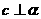 ,若
,若 ,则
,则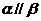
B.
 ,
,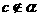 ,若
,若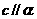 ,则
,则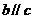
C.
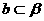 ,若
,若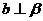 ,则
,则
D.
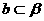 ,
,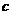 是
是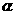 在
在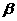 内的射影,若
内的射影,若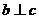 ,则
,则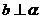
正解:C
C的逆命题是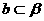 ,若
,若 ,则
,则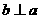 显然不成立。
显然不成立。
误解:选B。源于对C是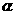 在
在 内的射影理不清。
内的射影理不清。

