4.[北 京 四 中2005年数学第一次统测(理科)]
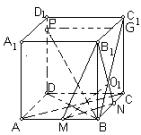
如图, 分别是正方体的棱
分别是正方体的棱 上的点.
(1)若
上的点.
(1)若 ,求证:无论点
,求证:无论点 在
在 上如何移动,总有
上如何移动,总有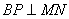 ;
(2)若
;
(2)若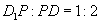 ,且
,且 平面
平面 ,求二面角
,求二面角 的大小.
的大小.
 4.(I)证法一:连AC、BD,则BD⊥AC,
∵
4.(I)证法一:连AC、BD,则BD⊥AC,
∵ , ∴MN//AC,∴BD⊥MN.
又∵DD1⊥平面ABCD,∴DD1⊥MN,
∴MN⊥平面BDD1.
∵无论点P在DD1上如何移动,总有BP
, ∴MN//AC,∴BD⊥MN.
又∵DD1⊥平面ABCD,∴DD1⊥MN,
∴MN⊥平面BDD1.
∵无论点P在DD1上如何移动,总有BP 平面BDD1,
故总有MN⊥BP.
证法二:连结AC、BD,则AC⊥BD.
∵
平面BDD1,
故总有MN⊥BP.
证法二:连结AC、BD,则AC⊥BD.
∵ , ∴MN//AC,∴ MN⊥BD,又PD⊥平面ABCD,
由三垂线定理得:MN⊥PB.
(II)解法一:过P作PG⊥C1C交CC1于G,连BG交B1N于O1,
∵PB⊥平面B1MN, ∴PB⊥B1N.
又∵PG⊥平面B1BCC1, ∴ BG⊥B1N,∴ΔBB1N≌ΔBCG,
∴ BN=CG,NC=GC1,
∴BN∶NC=DP∶PD1=2∶1.
同理BM∶MA=DP∶PD1=2∶1.
设AB=3a, 则BN=2a, ∴
, ∴MN//AC,∴ MN⊥BD,又PD⊥平面ABCD,
由三垂线定理得:MN⊥PB.
(II)解法一:过P作PG⊥C1C交CC1于G,连BG交B1N于O1,
∵PB⊥平面B1MN, ∴PB⊥B1N.
又∵PG⊥平面B1BCC1, ∴ BG⊥B1N,∴ΔBB1N≌ΔBCG,
∴ BN=CG,NC=GC1,
∴BN∶NC=DP∶PD1=2∶1.
同理BM∶MA=DP∶PD1=2∶1.
设AB=3a, 则BN=2a, ∴ ,
,
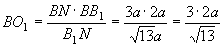 ,
连MO1,∵AB⊥平面B1BCC1, ∴ MO1⊥B1N,
∵∠MO1B就是二面角M-B1N-B的平面角,
,
连MO1,∵AB⊥平面B1BCC1, ∴ MO1⊥B1N,
∵∠MO1B就是二面角M-B1N-B的平面角,
 ,∴
,∴  .
解法二:设BD与MN相交于F,连结B1F,
∵PB⊥平面MNB1, ∴ PB⊥B1F,PB⊥MN,
∴在对角面BB1D1D内,ΔPBD∽ΔBB1F,
设BB1=DD1=3,则PD=2,
.
解法二:设BD与MN相交于F,连结B1F,
∵PB⊥平面MNB1, ∴ PB⊥B1F,PB⊥MN,
∴在对角面BB1D1D内,ΔPBD∽ΔBB1F,
设BB1=DD1=3,则PD=2, ,∴
,∴ , 即
, 即 ,故
,故 .
∵MN⊥PB,由三垂线定理得MN⊥BD,MN//AC,MN=2BF=
.
∵MN⊥PB,由三垂线定理得MN⊥BD,MN//AC,MN=2BF= , BN=2,
, BN=2,
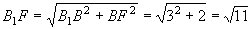 .
设二面角B-B1N-M的平面角为α,则
.
设二面角B-B1N-M的平面角为α,则 ,
,
 .
.
- 答案

