科目:,来源:,题型:
7. 某服务部门有n 个服务对象,每个服务对象是否需要服务是独立的,若每个服务对象一天中需要服务的可能性是 p , 则该部门一天中平均需要服务的对象个数是 ( )
A . n p (1-p) B. n p C. n D. p (1-p)
点击展开完整题目
试题详情
科目:,来源:,题型:
3.设15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为( )
A.15 B.10 C.20 D.5
|
ξ |
1 |
2 |
3 |
|
P |
0.4 |
0.2 |
0.4 |
点击展开完整题目
试题详情
科目:,来源:,题型:
22.(本小题满分14分)
已知函数: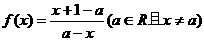
(1)求f(x)+f(2a-x)的值;
(2)当f(x)的定义域为[a+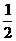 ,a+1]时,求f(x)的值域;
,a+1]时,求f(x)的值域;
(2)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值 .
点击展开完整题目
试题详情
科目:,来源:,题型:
21.(本小题满分12分)
设数列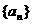 的首项a1=1,前n项和Sn满足关系
的首项a1=1,前n项和Sn满足关系
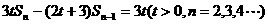 .
.
(1)求证:数列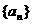 是等比数列;
是等比数列;
(2)设数列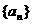 的公比是f(t),作数列
的公比是f(t),作数列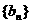 ,使
,使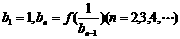 求bn;
求bn;
(3)求和:
点击展开完整题目
试题详情
科目:,来源:,题型:
20.(本题满分12分)
如图,△AOE和△BOE都是边长为1的等边三角形,
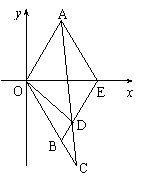 延长OB到C使|BC|=t(t>0),连AC交BE于D点.
延长OB到C使|BC|=t(t>0),连AC交BE于D点.
⑴用t表示向量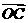 和
和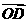 的坐标;
的坐标;
⑵当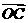 =
=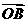 时,求向量
时,求向量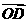 和
和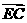 的夹角的大小.
的夹角的大小.
点击展开完整题目
试题详情

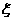 满足
满足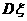 =2,则
=2,则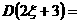 ( )
( )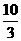 B.
B.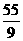 C.
C.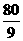 D.
D.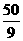
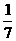 B.
B.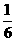 C.
C.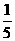 D.
D.