1. 设全集U={1, 3, 5, 7, 9},集合A={1, | a-5 | , 9}, CUA={5, 7}, 则a的值是 ( )
A. 2 B. 8 C. -2或8 D. 2或8
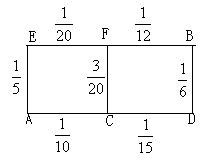
22.某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A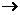 C
C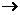 D算作两个路段:路段AC发生堵车事件的概率为
D算作两个路段:路段AC发生堵车事件的概率为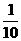 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为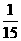 ).
).
(1) 请你为其选择一条由A到B的路线,使得
途中发生堵车事件的概率最小;
(2)
若记ξ路线A C
C F
F B中遇到堵车
B中遇到堵车
次数为随机变量ξ,求ξ的数学期望Eξ.
21.据气象预报,某地区下个月有小洪水的概率为0.25,有大洪水的概率为0.01。设工地上有台大型设备,为保护设备有以下三种方案。
方案1:运走设备,此时需花费3800元。
方案2:建一保护围墙,需花费2000元。但围墙无法防止大洪水,当大洪水来临,设备受损,损失费为60000元。
方案3:不采取措施,希望不发生洪水。此时大洪水来临损失60000元,小洪水来临损失10000元。
试比较哪一种方案好。
20.某车站每天8∶00~9∶00,9∶00~10∶00都恰有一辆客车到站,8∶00~9∶00到站的客车A可能在8∶10,8∶30,8∶50到站,其概率依次为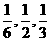 ;9∶00~10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为
;9∶00~10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为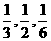 .
.
(1)
旅客甲8∶00到站,设他的候车时间为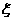 ,求
,求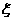 的分布列和
的分布列和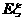 ;
;
(2)
旅客乙8∶20到站,设他的候车时间为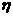 ,求
,求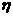 的分布列和
的分布列和 .
.
19.在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值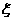 (元)的概率分布列和期望
(元)的概率分布列和期望 .
.
18.某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数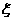 的分布列和
的分布列和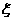 的期望,并求李明在一年内领到驾照的概率.
的期望,并求李明在一年内领到驾照的概率.
17.A、B两个试验方案在某科学试验中成功的概率相同,已知A、B两个方案至少一个成功的概率为0.36,
(1)求两个方案均获成功的概率;
(2)设试验成功的方案的个数为随机变量ξ,求ξ的分布列及数学期望.

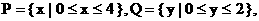 则下列对应中, 不是从P到Q的映射的
则下列对应中, 不是从P到Q的映射的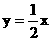 B.
B.
 C.
C.
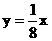 D.
D.
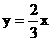
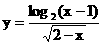 的定义域是
( )
的定义域是
( )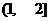 B.
(1,2) C. (2,+∞) D.
(-∞,2)
B.
(1,2) C. (2,+∞) D.
(-∞,2)