1. (如中)由平面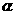 外一点P引平面的三条相等的斜线段,斜足分别为ABC,O为⊿ABC的外心,求证:
外一点P引平面的三条相等的斜线段,斜足分别为ABC,O为⊿ABC的外心,求证: 。
。
错解:因为O为⊿ABC的外心,所以OA=OB=OC,又因为PA=PB=PC,PO公用,所以⊿POA,⊿POB,⊿POC都全等,所以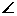 POA=
POA=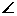 POB=
POB=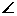 POC=RT
POC=RT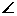 ,所以
,所以 。
。
错解分析:上述解法中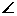 POA=
POA=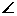 POB=
POB=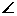 POC=RT
POC=RT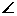 ,是对的,但它们为什么是直角呢?这里缺少必要的证明。
,是对的,但它们为什么是直角呢?这里缺少必要的证明。
正解:取BC的中点D,连PD,OD,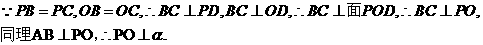
29.(案中)点P在直径为2的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和为最大值是
正确答案: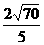
错误原因:找不到解题思路
28.(案中)在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是AB和AD的中点,则点A1到平面为EF的距离为
正确答案:
错误原因:不少学生能想到用等积法解,但运算存在严重问题。
27.(案中)四面体的一条棱长为x,其它各棱长为1,若把四面体的体积V表示成x的函数f(x),则f(x)的增区间为 ,减区间为 。
正确答案:(0,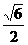
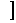
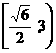
错误原因:不能正确写出目标函数,亦或者得到目标函数以后,不能注意x的隐藏范围。
26.(薛中)点P是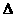 ABC所在平面外一点,且P在
ABC所在平面外一点,且P在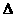 ABC三边距离相等,则P点在平面ABC上的射影是
ABC三边距离相等,则P点在平面ABC上的射影是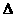 ABC的
心。
ABC的
心。
答案:内心或旁心
错解:内心
错因:P在平面ABC内的正射影可能在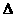 ABC内部,也可能在
ABC内部,也可能在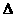 ABC外部。
ABC外部。
25.(薛中)异面直线a , b所成的角为 ,过空间一定点P,作直线L,使L与a ,b 所成的角均为
,过空间一定点P,作直线L,使L与a ,b 所成的角均为 ,这样的直线L有
条。
,这样的直线L有
条。
答案:三条
错解:一条
错因:没有能借助于平面衬托,思考问题欠严谨。过P作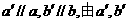 确定一平面
确定一平面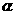 ,画
,画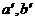 相交所成角的平分线m、g,过m, g分别作平面
相交所成角的平分线m、g,过m, g分别作平面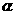 的垂面
的垂面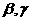 ,则在
,则在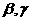 中易找到所求直线共有3条。
中易找到所求直线共有3条。
24.(薛中)已知直线L∩平面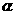 =O,A、B∈L,
=O,A、B∈L,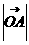 = 4 ,
= 4 ,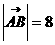 ;点A到平面
;点A到平面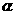 距离为1,则点B到平面
距离为1,则点B到平面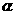 的距离为
。
的距离为
。
答案:1或3
错解:3
错因:考虑问题不全面,点A,B可能在点O的同侧,也可能在O点两侧。
23.(丁中)若 的中点
的中点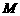 到平面
到平面 的距离为
的距离为 ,点
,点 到平面
到平面 的距离为
的距离为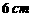 ,则点
,则点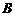 到平面
到平面 的距离为_________
的距离为_________ 。
。
错解:2
错因:没有注意到点A、B在平面 异侧的情况。
异侧的情况。
正解:2、14
22.(丁中)直线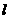 与平面α成角为300,
与平面α成角为300,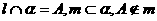 则m与
则m与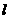 所成角的取值范围是
所成角的取值范围是
错解:[ 300 , 1200]
错因:忽视两条直线所成的角范围是
正解:[ 300 , 900]
21.(丁中)直二面角α-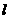 -β的棱
-β的棱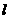 上有一点A,在平面α、β内各有一条射线AB,AC与
上有一点A,在平面α、β内各有一条射线AB,AC与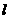 成450,AB
成450,AB ,则∠BAC=
。
,则∠BAC=
。
错解:600
错因:画图时只考虑一种情况
正解:600或1200

