3．解：(1)当　 (1分)

证明：取PD中点E，则EF//CD，且

∴四边形ABFE为平行四边形.　 (3分)

∴BF//AE. 又AE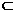平面PAD　 ∴BF//平面PAD　 (4分)

(2)平面ABCD，即是二面角的平

面角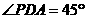　 (5分)

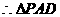为等腰直角三角形，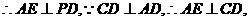

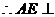平面PCD　 又BF//AE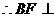，平面PCD. 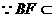平面PBC，

∴平面PCD⊥平面PBC，即二面角B-PC-D的大小为90°.　 (8分)

(3)在平面PCD内作EH⊥PC于点H，由平面PCD⊥平面PBC且平面PCD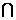

平面PBC=PC知：EH⊥平面PBC.　 (9分)

在，

在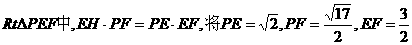代入得：

即点E到平面PBC的距离为　 (11分)

又点A到平面PBC的距离为(12分)