20.(江安中学)自半径为R的球面上一点P引球的两两垂直的弦PA、PB、PC,则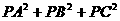 =_____。
=_____。
正解: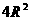 ,可将PA,PB,PC看成是球内接矩形的三度,则
,可将PA,PB,PC看成是球内接矩形的三度,则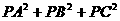 应是矩形对角线的平方,即球直径的平方。
应是矩形对角线的平方,即球直径的平方。
误解:没有考虑到球内接矩形,直接运算,易造成计算错误。
19.(江安中学)某地球仪上北纬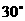 ,纬线的长度为
,纬线的长度为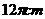 ,该地球仪的半径是_____cm,表面积是_____ cm2。
,该地球仪的半径是_____cm,表面积是_____ cm2。
正解: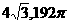
设地球仪的半径为R,纬线的半径为r 。
由已知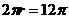 ,
,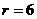
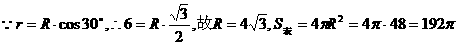 。
。
误解:误将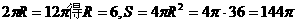
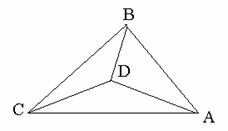
18.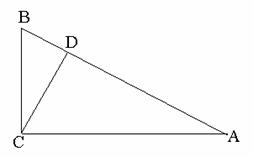 (江安中学)一个直角三角形的两条直角边长为2和4,沿斜边高线折成直三面角,则两直角边所夹角的余弦值为_____议程。
(江安中学)一个直角三角形的两条直角边长为2和4,沿斜边高线折成直三面角,则两直角边所夹角的余弦值为_____议程。
正解: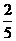 。
。
设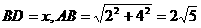
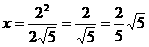
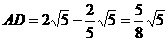
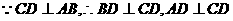
 为二面角的平面角,
为二面角的平面角,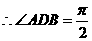
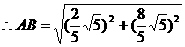
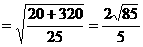
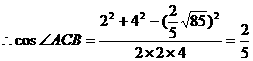
误解:折叠后仍然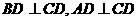 判断不了,找不到
判断不了,找不到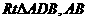 的长求不出。
的长求不出。
17.(蒲中)正方体AC1中,过点A作截面,使正方体的12条棱所在直线与截面所成的角都相等,试写出满足条件的一个截面____________
答案:面AD1C
点评:本题答案不唯一,可得12条棱分成三类:平行、相交、异面,考虑正三棱锥D-AD1C,易瞎猜。
16.(蒲中)已知三棱锥P-ABC的三条侧棱PA、PB、PC两两垂直,D是底面三角形内一点,且∠DPA=450,∠DPB=600,则∠DPC=__________
答案:600
点评:以PD为对角线构造长方体,问题转化为对角线PD与棱PC的夹角,利用cos2450+cos2600+cos2α=1得α=600,构造模型问题能力弱。
15.(蒲中)在平面角为600的二面角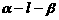 内有一点P,P到α、β的距离分别为PC=2cm,PD=3cm,则P到棱l的距离为____________
内有一点P,P到α、β的距离分别为PC=2cm,PD=3cm,则P到棱l的距离为____________
答案: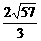 cm
cm
点评:将空间问题转化为平面问题利用正弦定理求解,转化能力较弱。
13.(磨中)把半径为r的四只小球全部放入一个大球内,则大球半径的最小值为__________。
正确答案:( )r
)r
错误原因:错误认为四个小球球心在同一平面上
12.(磨中)平面α与平面β相交成锐角θ,面α内一个圆在面β上的射影是离心率为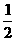 的椭圆,则角θ等于_______。
的椭圆,则角θ等于_______。

正确答案:30°
错误原因:分析不出哪些线段射影长不变,哪些线段射影长改变。
11.(磨中)△ABC是简易遮阳板,A、B是南北方向上两个定点,正东方向射出的太阳光线与地面成40°角,为使遮阴的阴影面ABD面积最大,遮阳板ABC与地面所成角应为_________。
正确答案:50°
错误原因:不会作图

 所在的平面,
所在的平面,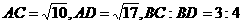 ,当
,当
