2025年金版新学案高中化学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版新学案高中化学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
典例1
用测压法在刚性密闭容器中研究$T^{\circ}C$时$4NO(g)\rightleftharpoons N_{2}(g)+2NO_{2}(g)$的分解反应,现将一定量的$NO$充入该密闭容器中,测得体系的总压强随时间的变化如下表所示:

(1) $20min$时,$NO$的转化率$\alpha=$
(2) $T^{\circ}C$时,$4NO(g)\rightleftharpoons N_{2}(g)+2NO_{2}(g)$反应的平衡常数$K_{p}=$
用测压法在刚性密闭容器中研究$T^{\circ}C$时$4NO(g)\rightleftharpoons N_{2}(g)+2NO_{2}(g)$的分解反应,现将一定量的$NO$充入该密闭容器中,测得体系的总压强随时间的变化如下表所示:

(1) $20min$时,$NO$的转化率$\alpha=$
48
%。(2) $T^{\circ}C$时,$4NO(g)\rightleftharpoons N_{2}(g)+2NO_{2}(g)$反应的平衡常数$K_{p}=$
0.1
( $K_{p}$为以分压表示的平衡常数)。
答案:
(1)48%
(2)0.1
解析:在恒温、恒容条件下,压强之比等于物质的量之比,因此可以直接用压强代替物质的量计算。
$4NO(g)\rightleftharpoons N_2(g)+2NO_2(g)$
开始的压强/MPa 15.00 0 0
转化的压强/MPa $4x$ $x$ $2x$
平衡的压强/MPa $15.00 - 4x$ $x$ $2x$
(1)20 min时,$15.00 - x = 13.2$,$x = 1.8$,NO的转化率为$\alpha = \frac{4×1.8}{15.00}×100\% = 48\%$。
(2)平衡时,$15.00 - x = 12.5$,$x = 2.5$,NO、$N_2$、$NO_2$的压强分别为5、2.5、5,代入公式$K_p = \frac{p(N_2)· p^2(NO_2)}{p^4(NO)} = \frac{2.5×5^2}{5^4} = 0.1$。
(1)48%
(2)0.1
解析:在恒温、恒容条件下,压强之比等于物质的量之比,因此可以直接用压强代替物质的量计算。
$4NO(g)\rightleftharpoons N_2(g)+2NO_2(g)$
开始的压强/MPa 15.00 0 0
转化的压强/MPa $4x$ $x$ $2x$
平衡的压强/MPa $15.00 - 4x$ $x$ $2x$
(1)20 min时,$15.00 - x = 13.2$,$x = 1.8$,NO的转化率为$\alpha = \frac{4×1.8}{15.00}×100\% = 48\%$。
(2)平衡时,$15.00 - x = 12.5$,$x = 2.5$,NO、$N_2$、$NO_2$的压强分别为5、2.5、5,代入公式$K_p = \frac{p(N_2)· p^2(NO_2)}{p^4(NO)} = \frac{2.5×5^2}{5^4} = 0.1$。
利用甲烷的裂解可以制得多种化工原料,甲烷裂解时发生的反应有:$2CH_{4}(g)\rightleftharpoons C_{2}H_{4}(g)+2H_{2}(g)$,$2CH_{4}(g)\rightleftharpoons C_{2}H_{2}(g)+3H_{2}(g)$。实验测得平衡时气体分压$(Pa)$与温度$(^{\circ}C)$之间的关系如图所示。$1725^{\circ}C$时,向$1L$恒容密闭容器中充入$0.3molCH_{4}$达到平衡,则反应$2CH_{4}(g)\rightleftharpoons C_{2}H_{4}(g)+2H_{2}(g)$的平衡常数$K_{p}=$
$1.0×10^7$ Pa
(用平衡分压代替平衡浓度),$CH_{4}$生成$C_{2}H_{2}$的平衡转化率为62.5%
。
答案:
$1.0×10^7$ Pa 62.5%
解析:由图可知,在1725℃时,$CH_4$的$\lg p = 2$,$C_2H_4$的$\lg p = 1$,$C_2H_2$的$\lg p = 2$,$H_2$的$\lg p = 5$,故$CH_4$的分压$p$为100 Pa,$C_2H_4$的分压$p$为10 Pa,$C_2H_2$的分压$p$为100 Pa,$H_2$的分压$p$为$10^5$ Pa,故反应$2CH_4(g)\rightleftharpoons C_2H_4(g)+2H_2(g)$的平衡常数$K_p = \frac{10×(10^5)^2}{100^2} = 1.0×10^7$;在同温同体积的条件下,气体的压强之比等于气体的物质的量之比,故$CH_4$、$C_2H_2$、$C_2H_4$的物质的量之比为$10:10:1$,根据C守恒,$CH_4$生成$C_2H_2$的平衡转化率为$\frac{10×2}{10 + 10×2 + 1×2}×100\% = 62.5\%$。
解析:由图可知,在1725℃时,$CH_4$的$\lg p = 2$,$C_2H_4$的$\lg p = 1$,$C_2H_2$的$\lg p = 2$,$H_2$的$\lg p = 5$,故$CH_4$的分压$p$为100 Pa,$C_2H_4$的分压$p$为10 Pa,$C_2H_2$的分压$p$为100 Pa,$H_2$的分压$p$为$10^5$ Pa,故反应$2CH_4(g)\rightleftharpoons C_2H_4(g)+2H_2(g)$的平衡常数$K_p = \frac{10×(10^5)^2}{100^2} = 1.0×10^7$;在同温同体积的条件下,气体的压强之比等于气体的物质的量之比,故$CH_4$、$C_2H_2$、$C_2H_4$的物质的量之比为$10:10:1$,根据C守恒,$CH_4$生成$C_2H_2$的平衡转化率为$\frac{10×2}{10 + 10×2 + 1×2}×100\% = 62.5\%$。
某温度下,$N_{2}O_{5}$气体在一体积固定的容器中发生如下反应:
$2N_{2}O_{5}(g)=4NO_{2}(g)+O_{2}(g)$(快反应) $\Delta H<0$
$2NO_{2}(g)\rightleftharpoons N_{2}O_{4}(g)$(慢反应) $\Delta H<0$,体系的总压强$p_{总}$和$p(O_{2})$随时间的变化如下图所示:
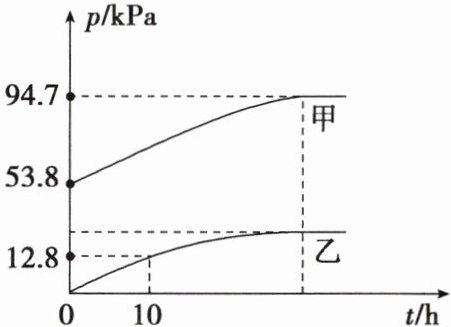
(1) 上图中表示$O_{2}$压强变化的曲线是
(2) 已知$N_{2}O_{5}$分解的反应速率$v = 0.12p(N_{2}O_{5})$ $(kPa· h^{-1})$,$t = 10h$时,$p(N_{2}O_{5})=$
(3) 该温度下$2NO_{2}\rightleftharpoons N_{2}O_{4}$反应的平衡常数$K_{p}=$
$2N_{2}O_{5}(g)=4NO_{2}(g)+O_{2}(g)$(快反应) $\Delta H<0$
$2NO_{2}(g)\rightleftharpoons N_{2}O_{4}(g)$(慢反应) $\Delta H<0$,体系的总压强$p_{总}$和$p(O_{2})$随时间的变化如下图所示:

(1) 上图中表示$O_{2}$压强变化的曲线是
乙
(填“甲”或“乙”)。(2) 已知$N_{2}O_{5}$分解的反应速率$v = 0.12p(N_{2}O_{5})$ $(kPa· h^{-1})$,$t = 10h$时,$p(N_{2}O_{5})=$
28.2
$kPa$,$v(N_{2}O_{5})=$______3.38
$kPa· h^{-1}$(结果保留两位小数,下同)。(3) 该温度下$2NO_{2}\rightleftharpoons N_{2}O_{4}$反应的平衡常数$K_{p}=$
0.05
$kPa^{-1}$($K_{p}$为以分压表示的平衡常数)。
答案:
(1)乙
(2)28.2 3.38
(3)0.05
解析:
(1)根据反应分析,随着反应的进行氧气的压强从0开始逐渐增大,所以乙为氧气的压强曲线;
(2)$t = 10$ h时,$p(O_2)=12.8$ kPa,由$2N_2O_5(g)\rightleftharpoons4NO_2(g)+O_2(g)$分析,反应的五氧化二氮的分压为25.6 kPa,起始压强为53.8 kPa,所以10 h时$p(N_2O_5)=(53.8 - 25.6)$ kPa = 28.2 kPa,$N_2O_5$分解的反应速率$v = \frac{0.12p(N_2O_5) kPa·h^{-1}}{ } = (0.12×28.2) kPa·h^{-1} = 3.38 kPa·h^{-1}$;
(3)因为$2N_2O_5(g)\rightleftharpoons4NO_2(g)+O_2(g)$,根据起始$p(N_2O_5)=53.8$ kPa,则$N_2O_5$完全分解时,生成的$p(NO_2)=107.6$ kPa,$p(O_2)=26.9$ kPa。
$2NO_2\rightleftharpoons N_2O_4$
起始分压(kPa) 107.6 0
改变分压(kPa) $2x$ $x$
平衡分压(kPa) $107.6 - 2x$ $x$
有$107.6 - 2x + x + 26.9 = 94.7$,解得$x = 39.8$ kPa,平衡常数$= \frac{39.8}{107.6 - 39.8×2} kPa^{-1} = 0.05 kPa^{-1}$。
(1)乙
(2)28.2 3.38
(3)0.05
解析:
(1)根据反应分析,随着反应的进行氧气的压强从0开始逐渐增大,所以乙为氧气的压强曲线;
(2)$t = 10$ h时,$p(O_2)=12.8$ kPa,由$2N_2O_5(g)\rightleftharpoons4NO_2(g)+O_2(g)$分析,反应的五氧化二氮的分压为25.6 kPa,起始压强为53.8 kPa,所以10 h时$p(N_2O_5)=(53.8 - 25.6)$ kPa = 28.2 kPa,$N_2O_5$分解的反应速率$v = \frac{0.12p(N_2O_5) kPa·h^{-1}}{ } = (0.12×28.2) kPa·h^{-1} = 3.38 kPa·h^{-1}$;
(3)因为$2N_2O_5(g)\rightleftharpoons4NO_2(g)+O_2(g)$,根据起始$p(N_2O_5)=53.8$ kPa,则$N_2O_5$完全分解时,生成的$p(NO_2)=107.6$ kPa,$p(O_2)=26.9$ kPa。
$2NO_2\rightleftharpoons N_2O_4$
起始分压(kPa) 107.6 0
改变分压(kPa) $2x$ $x$
平衡分压(kPa) $107.6 - 2x$ $x$
有$107.6 - 2x + x + 26.9 = 94.7$,解得$x = 39.8$ kPa,平衡常数$= \frac{39.8}{107.6 - 39.8×2} kPa^{-1} = 0.05 kPa^{-1}$。
查看更多完整答案,请扫码查看


