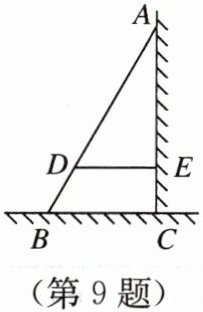
9. 如图,$ AB $ 是斜靠在墙上的长梯,梯脚 $ B $ 距墙脚 1.6 m,梯上点 $ D $ 距墙 1.4 m,$ BD $ 的长为 0.55 m,则梯子的长为 【
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
B
】
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
答案:
B
10. 化简 $ (a - 1)\sqrt{\frac{1}{1 - a}} $ 的结果是 【
A.$ \sqrt{1 - a} $
B.$ \sqrt{a - 1} $
C.$ \pm \sqrt{1 - a} $
D.$ -\sqrt{1 - a} $
D
】A.$ \sqrt{1 - a} $
B.$ \sqrt{a - 1} $
C.$ \pm \sqrt{1 - a} $
D.$ -\sqrt{1 - a} $
答案:
D
11. 二次根式 $ \sqrt{-(x + 2)^2} $ 在实数范围内有意义的条件是
x=-2
。
答案:
x=-2
12. 小华在解一元二次方程 $ x^2 - 4x = 0 $ 时,只得出一个根是 $ x = 4 $,则被他漏掉的另一个根是 $ x = $
0
。
答案:
0
13. 已知 $ y = \sqrt{x - 4} + \sqrt{4 - x} - 1 $,则 $ x^y + y^x = $
$\frac{5}{4}$
。
答案:
$\frac{5}{4}$
14. $ \sqrt{3} - \sqrt{2} $ 的倒数是
$\sqrt{3}+\sqrt{2}$
。
答案:
$\sqrt{3}+\sqrt{2}$
15. 已知最简二次根式 $ \sqrt[x - 2]{2y + 1} $ 和 $ \sqrt{x + 3} $ 是同类二次根式,则 $ \sqrt{x^2 + y^2} = $
5
。
答案:
5
16. 一元二次方程 $ x^2 - 6x - k = 0 $ 的一根是 2,则另一根是
4
,$ k = $-8
。
答案:
4,-8
17. 若 $ \frac{x}{2} = \frac{y}{7} = \frac{z}{5} $,$ x + y + z = 7 $,则 $ x = $
1
,$ y = $$\frac{7}{2}$
,$ z = $$\frac{5}{2}$
。
答案:
1,$\frac{7}{2}$,$\frac{5}{2}$
18. 用配方法解一元二次方程:$ 3x^2 - 6x = 48 $。第一步化二次项系数为 1,得
$x^{2}-2x=16$
,方程两边同时加1
,配方得$(x-1)^{2}=17$
。
答案:
$x^{2}-2x=16$,1,$(x-1)^{2}=17$
19. 矩形的长和宽分别是 $ \sqrt{15} $ 和 $ \sqrt{6} $,则矩形的面积是
$3\sqrt{10}$
。
答案:
$3\sqrt{10}$
20. 当 $ k $
$\geqslant -\frac{9}{8}$
时,关于 $ x $ 的方程 $ 2x^2 - (4k + 1)x + 2k^2 - 1 = 0 $ 有两个实数根。
答案:
$\geqslant -\frac{9}{8}$
21. (5分)计算:$ \sqrt{12} - \sqrt{18} - \sqrt{0.5} + \sqrt{\frac{1}{3}} $。
答案:
原式$=2\sqrt{3}-3\sqrt{2}-\sqrt{\frac{1}{2}}+\sqrt{\frac{1× 3}{3× 3}}=2\sqrt{3}-3\sqrt{2}-\sqrt{\frac{1× 2}{2× 2}}+\frac{\sqrt{3}}{3}=\frac{7}{3}\sqrt{3}-3\sqrt{2}-\frac{\sqrt{2}}{2}=\frac{7}{3}\sqrt{3}-\frac{7}{2}\sqrt{2}$
查看更多完整答案,请扫码查看


