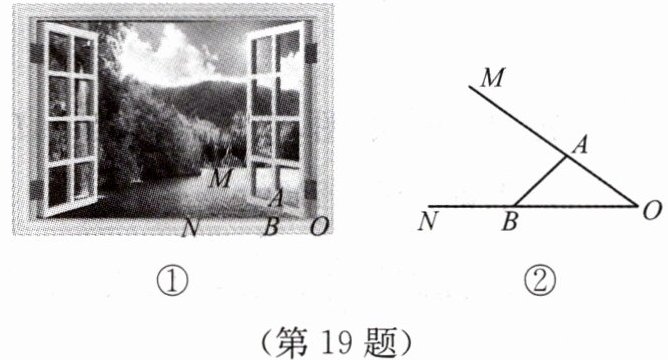
19. (10 分)为了同学们的身体健康,学校需要做到经常开窗通风.如图①,一扇窗户打开一定角度,其中一端固定在窗户边$OM上的点A$处,另一端$B在边ON$上滑动,如图②为某一位置从上往下看的平面图,测得此时$\angle ABO = 45^{\circ}$,$AB$的长为 20 cm.(结果精确到 1 cm,参考数据:$\sin 37^{\circ} \approx 0.6$,$\cos 37^{\circ} \approx 0.8$,$\tan 37^{\circ} \approx 0.75$,$\sqrt{2} \approx 1.414$)
(1)求固定点$A到窗框OB$的距离;
(2)若测得$\angle AOB = 37^{\circ}$,求$OA$的长度.
(1)求固定点$A到窗框OB$的距离;
(2)若测得$\angle AOB = 37^{\circ}$,求$OA$的长度.

答案:
(1)如图,过点$A$作$AD\perp ON$于点$D$.在$Rt\triangle ABD$中,$\angle ABO=45^{\circ}$,$AB=20\ cm$,则$AD=AB\cdot \sin \angle ABO=20\sin 45^{\circ}=10\sqrt{2}\approx 14.14\approx 14(cm)$.
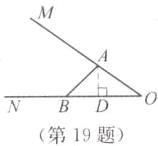
(2)如图,由
(1)已知,$AD=10\sqrt{2}\ cm$.在$Rt\triangle AOD$中,$OA=\frac{AD}{\sin \angle AOB}=\frac{10\sqrt{2}}{\sin 37^{\circ}}\approx \frac{10× 1.414}{0.6}\approx 24(cm)$
(1)如图,过点$A$作$AD\perp ON$于点$D$.在$Rt\triangle ABD$中,$\angle ABO=45^{\circ}$,$AB=20\ cm$,则$AD=AB\cdot \sin \angle ABO=20\sin 45^{\circ}=10\sqrt{2}\approx 14.14\approx 14(cm)$.

(2)如图,由
(1)已知,$AD=10\sqrt{2}\ cm$.在$Rt\triangle AOD$中,$OA=\frac{AD}{\sin \angle AOB}=\frac{10\sqrt{2}}{\sin 37^{\circ}}\approx \frac{10× 1.414}{0.6}\approx 24(cm)$
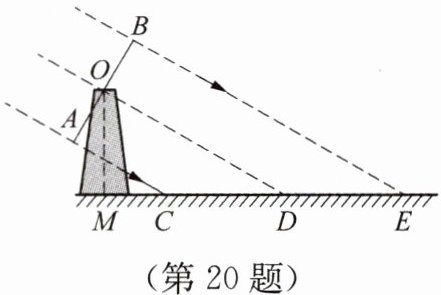
20. (10 分)如图是某风车平面示意图,其相同的四个叶片均匀分布,水平地面上的点$M在旋转中心O$的正下方.某一时刻,太阳光线恰好垂直照射叶片$OA$、$OB$,此时各叶片影子在点$M右侧形成线段CE$,点$O的对应点为点D$,测得$MC = 4\ m$,$CE = 16\ m$,此时太阳与地面的夹角为$30^{\circ}$(即$\angle ODM = 30^{\circ}$).
(1)求旋转中心到地面的距离$OM$的值;
(2)风车转动时,要求叶片外端离地面的最低高度高于 2.5 m,请判断此风车是否符合要求.
(1)求旋转中心到地面的距离$OM$的值;
(2)风车转动时,要求叶片外端离地面的最低高度高于 2.5 m,请判断此风车是否符合要求.

答案:
(1)由题意,得$AC// OD// BE$,$AO=BO$,$CE=16\ m$,$\therefore \frac{OA}{OB}=\frac{CD}{DE}=1$.$\therefore CD=DE=\frac{1}{2}CE=8(m)$.$\because MC=4\ m$,$\therefore MD=MC+CD=12\ m$.$\because \angle ODM=30^{\circ}$,$\therefore OM=MD\tan 30^{\circ}=12\tan 30^{\circ}=4\sqrt{3}(m)$.

(2)如图,过点$C$作$CF\perp OD$,垂足为$F$,则四边形$AOFC$为矩形.$\because \angle FDC=30^{\circ}$,$CD=8\ m$,$\therefore CF=CD\sin 30^{\circ}=4(m)$,即$OA=4\ m$.$\therefore$叶片外端离地面的最低高度为$(4\sqrt{3}-4)m$.$\because 4\sqrt{3}-4\geqslant 2.5$,$\therefore$此风车符合要求
(1)由题意,得$AC// OD// BE$,$AO=BO$,$CE=16\ m$,$\therefore \frac{OA}{OB}=\frac{CD}{DE}=1$.$\therefore CD=DE=\frac{1}{2}CE=8(m)$.$\because MC=4\ m$,$\therefore MD=MC+CD=12\ m$.$\because \angle ODM=30^{\circ}$,$\therefore OM=MD\tan 30^{\circ}=12\tan 30^{\circ}=4\sqrt{3}(m)$.

(2)如图,过点$C$作$CF\perp OD$,垂足为$F$,则四边形$AOFC$为矩形.$\because \angle FDC=30^{\circ}$,$CD=8\ m$,$\therefore CF=CD\sin 30^{\circ}=4(m)$,即$OA=4\ m$.$\therefore$叶片外端离地面的最低高度为$(4\sqrt{3}-4)m$.$\because 4\sqrt{3}-4\geqslant 2.5$,$\therefore$此风车符合要求
查看更多完整答案,请扫码查看


