13. 如图,圆桌正上方的灯(看作一个点)发出的光线照射桌面后,在地面上形成阴影。已知桌面的直径为$1.2m$,桌面距离地面$1m$。若灯泡距离地面$3m$,则地面上阴影部分的面积为

$0.81\pi\ m^2$
。
答案:
$0.81\pi\ m^2$
14. 如图,点$A的坐标为(-3,5)$,$\triangle EDC是由\triangle ABC$缩小后得到的,那么点$E$的坐标是
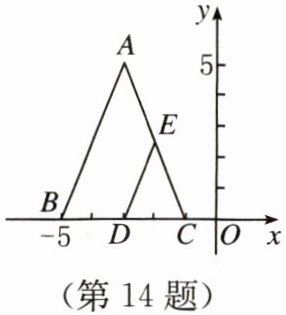
$(-2,2.5)$
。
答案:
$(-2,2.5)$
15. 如图,$\triangle ABC的周长是a$,顺次连结各边中点得$\triangle A_1B_1C_1$,再顺次连结$\triangle A_1B_1C_1各边中点得\triangle A_2B_2C_2$,……依次类推,则$\triangle A_{2011}B_{2011}C_{2011}$的周长是

$\frac{a}{2^{2011}}$
。
答案:
$\frac{a}{2^{2011}}$
16.(8分)如图,已知$\triangle ABC和点O$,以点$O$为位似中心,画出$\triangle ABC的位似图形\triangle A'B'C'$,其位似比为$1:2$。


答案:
答案略
17.(10分)已知线段$a$、$b$、$c满足\frac{a}{3} = \frac{b}{2} = \frac{c}{6}$,且$a + 2b + c = 26$。
(1)判断$a$、$2b$、$c$、$b^2$是否成比例;
(2)若实数$x为a$、$b$的比例中项,求$x$的值。
(1)判断$a$、$2b$、$c$、$b^2$是否成比例;
(2)若实数$x为a$、$b$的比例中项,求$x$的值。
答案:
(1)设$\frac{a}{3}=\frac{b}{2}=\frac{c}{6}=k$,则$a=3k$,$b=2k$,$c=6k$. $\because\ a+2b+c=26$,$\therefore\ 3k+2×2k+6k=26$,即$13k=26$,解得$k=2$. $\therefore\ a=6$,$b=4$,$c=12$. $\therefore\ a$、$2b$、$c$、$b^2$分别为6、8、12、16. $\because\ \frac{6}{8}=\frac{12}{16}=\frac{3}{4}$,$\therefore\ a$、$2b$、$c$、$b^2$成比例.
(2)$\because\ \frac{6}{x}=\frac{x}{4}$,$\therefore\ x^2=24$. $\therefore\ x=\pm2\sqrt{6}$.
(1)设$\frac{a}{3}=\frac{b}{2}=\frac{c}{6}=k$,则$a=3k$,$b=2k$,$c=6k$. $\because\ a+2b+c=26$,$\therefore\ 3k+2×2k+6k=26$,即$13k=26$,解得$k=2$. $\therefore\ a=6$,$b=4$,$c=12$. $\therefore\ a$、$2b$、$c$、$b^2$分别为6、8、12、16. $\because\ \frac{6}{8}=\frac{12}{16}=\frac{3}{4}$,$\therefore\ a$、$2b$、$c$、$b^2$成比例.
(2)$\because\ \frac{6}{x}=\frac{x}{4}$,$\therefore\ x^2=24$. $\therefore\ x=\pm2\sqrt{6}$.
查看更多完整答案,请扫码查看


