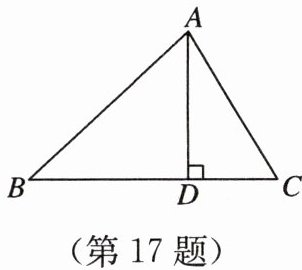
17. (10 分)如图,在$\triangle ABC$中,$AD是BC$上的高,$\tan B = \cos \angle DAC$.
(1)求证:$AC = BD$;
(2)若$\sin C = \frac{12}{13}$,$BC = 12$,求$AD$的长.
(1)求证:$AC = BD$;
(2)若$\sin C = \frac{12}{13}$,$BC = 12$,求$AD$的长.

答案:
(1)证明:$\because AD$是$BC$上的高,$\therefore AD\perp BC$,$\therefore \angle ADB=90^{\circ}$,$\angle ADC=90^{\circ}$.在$Rt\triangle ABD$和$Rt\triangle ADC$中,$\because \tan B=\frac{AD}{BD}$,$\cos \angle DAC=\frac{AD}{AC}$,又已知$\tan B=\cos \angle DAC$,$\therefore \frac{AD}{BD}=\frac{AD}{AC}$,$\therefore AC=BD$;
(2)$AD=8$
(1)证明:$\because AD$是$BC$上的高,$\therefore AD\perp BC$,$\therefore \angle ADB=90^{\circ}$,$\angle ADC=90^{\circ}$.在$Rt\triangle ABD$和$Rt\triangle ADC$中,$\because \tan B=\frac{AD}{BD}$,$\cos \angle DAC=\frac{AD}{AC}$,又已知$\tan B=\cos \angle DAC$,$\therefore \frac{AD}{BD}=\frac{AD}{AC}$,$\therefore AC=BD$;
(2)$AD=8$
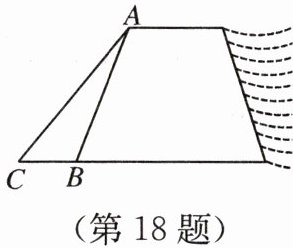
18. (10 分)如图,一大坝改造,将坝堤的背水坡的坡底加宽,使坡度为$\sqrt{3}:1的斜坡AB变为坡度为1:1的斜坡AC$,已知斜坡$AB$的长为 100 m,求$CB$的长.(结果保留根号)

答案:
$50(\sqrt{3}-1)\ m$
查看更多完整答案,请扫码查看


