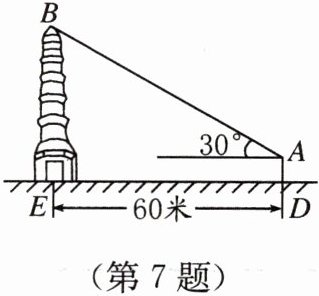
7. 如图,小强和小明去测量一座古塔的高度,他们在离古塔 60 米的$A$处,用测角仪器测得古塔顶的仰角为$30^{\circ}$,已知仰角仪器高$AD = 1.5$米,则古塔$BE$的高为 【
A.$(20\sqrt{3} - 1.5)$米
B.$(20\sqrt{3} + 1.5)$米
C.31.5 米
D.28.5 米
B
】
A.$(20\sqrt{3} - 1.5)$米
B.$(20\sqrt{3} + 1.5)$米
C.31.5 米
D.28.5 米
答案:
B
8. $\triangle ABC$的周长是 60 cm,若$\angle C = 90^{\circ}$,$\tan A = \frac{12}{5}$,则$\triangle ABC$的面积是 【
A.$30\ cm^2$
B.$60\ cm^2$
C.$120\ cm^2$
D.$240\ cm^2$
C
】A.$30\ cm^2$
B.$60\ cm^2$
C.$120\ cm^2$
D.$240\ cm^2$
答案:
C
9. 若$\triangle ABC$是等边三角形,且中线长是$m$,则$\triangle ABC$的边长是 【
A.$\sqrt{3}m$
B.$\frac{\sqrt{3}}{3}m$
C.$\frac{2\sqrt{3}}{3}m$
D.$2\sqrt{3}m$
C
】A.$\sqrt{3}m$
B.$\frac{\sqrt{3}}{3}m$
C.$\frac{2\sqrt{3}}{3}m$
D.$2\sqrt{3}m$
答案:
C
10. 在直角三角形中,斜边$AB是直角边BC$的 3 倍,则$\cos A$是 【
A.$\frac{2\sqrt{2}}{3}$
B.$2\sqrt{3}$
C.$\frac{\sqrt{3}}{6}$
D.$\frac{\sqrt{6}}{3}$
A
】A.$\frac{2\sqrt{2}}{3}$
B.$2\sqrt{3}$
C.$\frac{\sqrt{3}}{6}$
D.$\frac{\sqrt{6}}{3}$
答案:
A
11. 如果两个相似三角形的相似比是$3:5$,周长的差是 4 cm,那么较大三角形的周长为
10
cm.
答案:
10
12. 若直角三角形两条直角边长分别为 5 和 12,则斜边上的中线长为
$\frac{13}{2}$
.
答案:
$\frac{13}{2}$
13. 若等腰直角三角形的一边长是 2,则它的面积为
2或1
.
答案:
2或1
14. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$BC = 6$,$AC = 8$,则$\sin A = $
$\frac{3}{5}$
.
答案:
$\frac{3}{5}$
15. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\sin B = \frac{5}{13}$,则$\cos B = $
$\frac{12}{13}$
.
答案:
$\frac{12}{13}$
16. (10 分)计算:
(1)$\sqrt{2}\sin 45^{\circ} + \cos 30^{\circ} \cdot \tan 60^{\circ} - \sqrt{(-3)^2}$;
(2)$(2 - \sin 60^{\circ})^0 + (\frac{1}{2})^{-1} - (\sqrt{3})^2 + | - \tan 45^{\circ}|$.
(1)$\sqrt{2}\sin 45^{\circ} + \cos 30^{\circ} \cdot \tan 60^{\circ} - \sqrt{(-3)^2}$;
(2)$(2 - \sin 60^{\circ})^0 + (\frac{1}{2})^{-1} - (\sqrt{3})^2 + | - \tan 45^{\circ}|$.
答案:
(1)原式$=\sqrt{2}× \frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}× \sqrt{3}-\sqrt{9}=\frac{2}{2}+\frac{3}{2}-3=-\frac{1}{2}$;
(2)原式$=(2-\frac{\sqrt{3}}{2})^{0}+2-3+|-1|=1+2-3+1=1$
(1)原式$=\sqrt{2}× \frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}× \sqrt{3}-\sqrt{9}=\frac{2}{2}+\frac{3}{2}-3=-\frac{1}{2}$;
(2)原式$=(2-\frac{\sqrt{3}}{2})^{0}+2-3+|-1|=1+2-3+1=1$
查看更多完整答案,请扫码查看


