第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. [2025·青岛即墨区模拟]在实数$\frac{\pi}{2},\sqrt{2},\frac{22}{7},\sqrt[3]{9},$0.101 001 000 1中,无理数有(
A.2个
B.3个
C.4个
D.5个
B
)A.2个
B.3个
C.4个
D.5个
答案:
B
2. [2025·淄博淄川区期末]把下列各数填入相应的集合内:7.5,$\sqrt{15}$,4,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,$\sqrt[3]{-27}$,0.31,$- \pi$,$0.\dot{1}\dot{5}$.
有理数集合:$\{ $
无理数集合:$\{ $
正实数集合:$\{ $
负实数集合:$\{ $
有理数集合:$\{ $
7.5,4,$\frac{2}{3}$,$\sqrt[3]{-27}$,0.31,$0.\dot{1}\dot{5}$
$\cdots \}$; 无理数集合:$\{ $
$\sqrt{15}$,$\sqrt{\frac{9}{17}}$,$- \pi$
$\cdots \}$; 正实数集合:$\{ $
7.5,$\sqrt{15}$,4,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,0.31,$0.\dot{1}\dot{5}$
$\cdots \}$; 负实数集合:$\{ $
$\sqrt[3]{-27}$,$- \pi$
$\cdots \}$.
答案:
【解】有理数集合:$\{ 7.5,4,\frac {2}{3},\sqrt [3]{-27},0.31,0.\dot {1}\dot {5},... \} ;$ 无理数集合:$\{ \sqrt {15},\sqrt {\frac {9}{17}},-π,... \} ;$ 正实数集合:$\{ 7.5,\sqrt {15},4,\sqrt {\frac {9}{17}},\frac {2}{3},0.31,0.\dot {1}\dot {5},... \} ;$ 负实数集合:$\{ \sqrt [3]{-27},-π,... \} .$
3. [2025·重庆月考]下列数中没有倒数的是(
A.0
B.$\pi$
C.$\sqrt{2}$
D.$(-3)^0$
A
)A.0
B.$\pi$
C.$\sqrt{2}$
D.$(-3)^0$
答案:
A
4. 下列各组数中,互为相反数的是(
A.$-2$和$\frac{1}{2}$
B.$\sqrt{(-2)^2}$与$\sqrt[3]{-8}$
C.$\left| - \sqrt{2} \right|$与$\sqrt{2}$
D.$- \sqrt[3]{8}$与$\sqrt[3]{-8}$
B
)A.$-2$和$\frac{1}{2}$
B.$\sqrt{(-2)^2}$与$\sqrt[3]{-8}$
C.$\left| - \sqrt{2} \right|$与$\sqrt{2}$
D.$- \sqrt[3]{8}$与$\sqrt[3]{-8}$
答案:
B
5. $\sqrt{5} - 3$的绝对值是(
A.$\sqrt{5} - 3$
B.$3 - \sqrt{5}$
C.$- \sqrt{5} - 3$
D.$\sqrt{5} + 3$
B
)A.$\sqrt{5} - 3$
B.$3 - \sqrt{5}$
C.$- \sqrt{5} - 3$
D.$\sqrt{5} + 3$
答案:
B
6. 数轴上点P的位置如图所示,则点P表示的数可能是(

A.$\frac{2}{3}$
B.$- \sqrt{3}$
C.$\sqrt{3}$
D.$\sqrt[3]{8}$
C
)
A.$\frac{2}{3}$
B.$- \sqrt{3}$
C.$\sqrt{3}$
D.$\sqrt[3]{8}$
答案:
C
7. 如图,在数轴上点A,点D所对应的数分别为3,1,点O为原点,$BA \perp OA$,$AB = 1$,以D为圆心,DB的长为半径的圆弧交数轴于点C,则点C在数轴上所对应的数是(
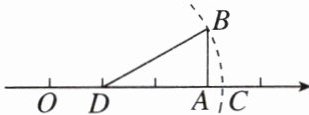
A.$\sqrt{3} + 1$
B.$\sqrt{5} + 1$
C.$\sqrt{10}$
D.$\sqrt{10} + 1$
B
)
A.$\sqrt{3} + 1$
B.$\sqrt{5} + 1$
C.$\sqrt{10}$
D.$\sqrt{10} + 1$
答案:
B
8. 母题教材P116随堂练习T4(1)在数轴上作出$- \sqrt{8}$的对应点.
(2)请在数轴上表示出$\sqrt{5} - 2$.
(2)请在数轴上表示出$\sqrt{5} - 2$.
答案:
【解】
(1)如图,点C即为所求.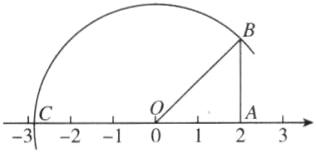
(2)如图,点C为所求作的表示$\sqrt{5}$−2的点.
【解】
(1)如图,点C即为所求.

(2)如图,点C为所求作的表示$\sqrt{5}$−2的点.

9. [2025·聊城模拟]下列说法:
①数轴上有无数多个表示无理数的点;
②带根号的数不一定是无理数;
③每个有理数都可以用数轴上唯一的点来表示;
④无理数的倒数不是无理数;
⑤没有最大的负实数,但有最小的正实数;
⑥两个有理数比较,绝对值大的反而小.
其中正确的有(
A.①②③
B.②③④
C.③④⑤
D.①⑤⑥
①数轴上有无数多个表示无理数的点;
②带根号的数不一定是无理数;
③每个有理数都可以用数轴上唯一的点来表示;
④无理数的倒数不是无理数;
⑤没有最大的负实数,但有最小的正实数;
⑥两个有理数比较,绝对值大的反而小.
其中正确的有(
A
)A.①②③
B.②③④
C.③④⑤
D.①⑤⑥
答案:
A
10. 如图,在数轴上,$AB = AC$,A,B两点对应的实数分别是1,$\sqrt{3}$,则点C对应的实数是(
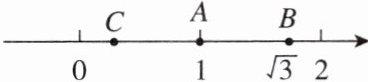
A.$\sqrt{3} - 1$
B.$1 - \sqrt{3}$
C.$2 - \sqrt{3}$
D.$\sqrt{3} - 2$
C
)
A.$\sqrt{3} - 1$
B.$1 - \sqrt{3}$
C.$2 - \sqrt{3}$
D.$\sqrt{3} - 2$
答案:
C
查看更多完整答案,请扫码查看


