《2025年综合应用创新题典中点七年级数学上册鲁教版五四制》

10. 如图，AD和BE是△ABC的中线，则以下结论：①AE=CE；②O是△ABC的重心；③△ABD与△ACD的面积相等；④过C，O两点的直线平分线段AB；⑤∠ABE=∠CBE；⑥AD=BE，其中正确的结论是（B）

A.①②③⑤
B.①②③④
C.②③④⑥
D.①②⑤⑥

答案： B　【点拨】因为AD和BE是△ABC的中线，所以AE=CE,BD=CD,点O是△ABC的重心,故①②正确;由BD=CD,可得$S_{△ABD}=S_{△ACD}$,故③正确;由点O是△ABC的重心,可得过C,O两点的直线平分线段AB,故④正确;根据已知条件无法得出∠ABE=∠CBE,AD=BE,故⑤⑥错误.

11. 新考法 整体思想 如图，BE，CF都是△ABC的角平分线，且∠BDC=115°，则∠A=（50°）

A.50°
B.45°
C.65°
D.70°

答案： A　【点拨】因为∠EBC+∠FCB+∠BDC=180°,∠BDC=115°,所以∠EBC+∠FCB=65°.因为BE,CF都是△ABC的角平分线，所以∠EBC=$\frac{1}{2}$∠ABC,∠BCF=$\frac{1}{2}$∠ACB.所以∠ABC+∠ACB=2(∠EBC+∠FCB)=130°.所以∠A=180°−(∠ABC+∠ACB)=50°.

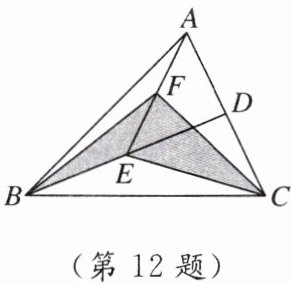
12. 如图，BD是△ABC的边AC上的中线，AE是△ABD的边BD上的中线，BF是△ABE的边AE上的中线，若△ABC的面积是32，则阴影部分的面积是（12）

A.12
B.18
C.8
D.206

答案： A　【点拨】因为BD是△ABC的边AC上的中线,$S_{△ABC}=32$,所以$S_{△ABD}=S_{△BCD}=\frac{1}{2}S_{△ABC}=16$.因为AE是△ABD的边BD上的中线，所以$S_{△ABE}=S_{△AED}=\frac{1}{2}S_{△ABD}=8$.因为BF是△ABE 的边AE上的中线,所以$S_{△ABF}=S_{△BEF}=\frac{1}{2}S_{△ABE}=\frac{1}{2}×8=4$.同理可得,$S_{△EFC}=\frac{1}{2}S_{△AEC}=\frac{1}{2}×16=8$,所以$S_{阴影部分}=S_{△BEF}+S_{△EFC}=4+8=12$.

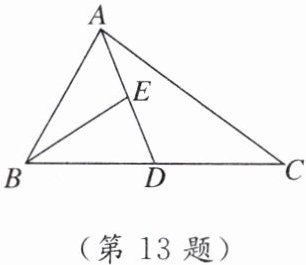
13. 如图，AD是△ABC的中线，BE是△ABD的中线.若△ABC的面积为20，BD=5，则点E到BC边的距离为_______.

]

答案：
2　【点拨】如图，过点E作BD的垂线,交BD于点H.因为AD是△ABC的中线，所以$S_{△ABD}=\frac{1}{2}S_{△ABC}$.因为BE是△ABD的中线,所以$S_{△BED}=\frac{1}{2}S_{△ABD}=\frac{1}{4}S_{△ABC}$.因为△ABC的面积为20,所以△EBD的面积是5,所以$\frac{1}{2}BD·EH=5$,即$\frac{1}{2}×5·EH=5$,所以EH=2,即点E 到BC边的距离为2.

14. 新考法 分类讨论法 如图，在△ABC中（AB＞BC），AC=2BC，BC边上的中线AD把△ABC的周长分成60和40两部分，则AC=48，AB=28.

答案： 48;28　【点拨】因为AD是△ABC的边BC上的中线,所以BD=CD,设BD=CD=x,AB=y,则AC=2BC=4x,存在两种情况:①AC+CD=60,AB+BD=40,则4x+x=60,x+y=40,解得x=12,y=28,所以AC=4x=48,AB=28;②AC+CD=40,AB+BD=60,则4x+x=40,x+y=60,解得x=8,y=52,所以AC=4x=32,AB=52,BC=2x=16,此时不符合三角形三边关系;综上,AC=48,AB=28.

15. [2025·济宁模拟]如图，在△ABC中，AE是边BC上的中线，AD⊥BC交BC于点D，F为AB的中点，连接EF.已知AD=6，△ABC的面积为24.
(1)求CE的长.
(2)若AE=7，求△AEF与△BEF的周长差.
]

答案： 【解】
(1)因为AD=6,△ABC的面积为24,AD⊥BC,所以$\frac{1}{2}AD·BC=\frac{1}{2}×6BC=24$,解得BC=8.因为AE是△ABC的边BC上的中线,所以CE=BE=$\frac{1}{2}BC=4$.
(2)因为F为AB的中点,所以AF=BF.因为△AEF的周长=AE+EF+AF=AE+EF+BF,△BEF的周长=BE+EF+BF,所以△AEF与△BEF的周长差=AE−BE=7−4=3.

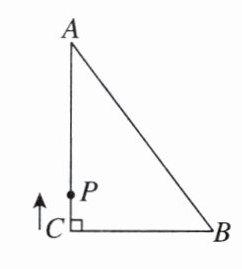
16. 新视角 动点探究题 如图，在△ABC中，∠C=90°，AC=8 cm，BC=6 cm，AB=10 cm.若动点P从点C开始，按C→A→B→C的路径运动，且速度为2 cm/s.设点P运动的时间为t s.
(1)若CP把△ABC的周长分成相等的两部分，求t的值；
(2)若CP把△ABC的面积分成相等的两部分，求t的值；
(3)若△BCP的面积为12 cm²，求t的值.

]

答案： 【解】
(1)在△ABC中,因为AC=8cm,BC=6cm,AB=10cm,所以△ABC的周长=8+6+10=24(cm),所以当CP把△ABC的周长分成相等的两部分时,点P在AB上,且CA+AP=BP+BC=12cm,所以2t=12,所以t=6.
(2)易知当点P在AB的中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+10÷2=13(cm),所以2t=13,所以t=6.5.
(3)分两种情况:①当点P在AC上时，因为△BCP 的面积为12cm²,所以$\frac{1}{2}×6CP=12$,所以CP=4cm,所以2t=4,所以t=2.②当点P在AB上时，因为△BCP的面积为12cm²,△ABC的面积为$\frac{1}{2}×6×8=24(cm²)$,所以△ABC的面积为△BCP面积的2倍.所以点P为AB的中点,由
(2)知此时t=6.5.综上,当t为2或6.5时,△BCP的面积为12cm².