第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
7. 如图,课间小林拿着老师的等腰直角三角板玩,不小心将其掉到两张凳子之间(凳子与地面垂直),已知 $ DC = 55 $ cm,$ CE = 75 $ cm,则两张凳子的高度之和为
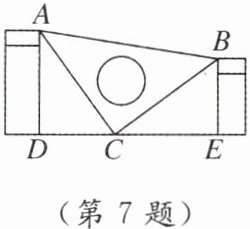
130
cm.
答案:
130 【点拨】由题意得$AC=BC,∠ACB=90^{\circ },$$AD⊥DE,BE⊥DE$,所以$∠ADC=∠CEB=90^{\circ },$
所以$∠ACD+∠DAC=∠ACD+∠BCE=90^{\circ },$
所以$∠DAC=∠ECB$,所以$△ADC\cong △CEB$
(AAS),所以$AD=CE=75cm,BE=CD=55cm$,所以两张凳子的高度之和为$AD+BE=$$75+55=130(cm).$
所以$∠ACD+∠DAC=∠ACD+∠BCE=90^{\circ },$
所以$∠DAC=∠ECB$,所以$△ADC\cong △CEB$
(AAS),所以$AD=CE=75cm,BE=CD=55cm$,所以两张凳子的高度之和为$AD+BE=$$75+55=130(cm).$
8. 小明用同种材料制成的金属框架如图所示,已知 $ \angle B = \angle E $,$ AB = DE $,$ BF = EC $,其中框架 $ \triangle ABC $ 的质量为 $ 840 $ g,$ CF $ 的质量为 $ 106 $ g,则整个金属框架的质量为 (
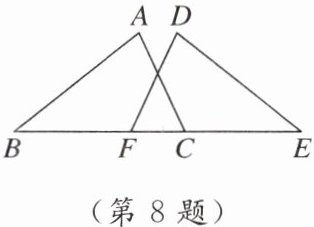
A.$ 734 $ g
B.$ 946 $ g
C.$ 1052 $ g
D.$ 1574 $ g
D
)
A.$ 734 $ g
B.$ 946 $ g
C.$ 1052 $ g
D.$ 1574 $ g
答案:
D 【点拨】因为$BF=EC$,所以$BC=EF$. 因为$∠B=∠E,AB=DE$,所以$△ABC\cong △DEF$
(SAS),所以整个金属框架的质量为$840×2-$$106=1574(g)$. 故选 D.
(SAS),所以整个金属框架的质量为$840×2-$$106=1574(g)$. 故选 D.
9. 学习《利用三角形全等测距离》后,“开拓”小组的同学就“测量河两岸 $ A $,$ B $ 两点间距离”这一问题,设计了如下方案:如图,在点 $ B $ 所在河岸的同侧平地上取点 $ C $ 和点 $ D $. 使点 $ A $,$ B $,$ C $ 在一条直线上,且 $ CD = BC $,测得 $ \angle DCB = 100^{\circ} $,$ \angle ADC = 65^{\circ} $,在 $ CD $ 的延长线上取一点 $ E $,使 $ \angle BEC = 15^{\circ} $,这时测得 $ DE $ 的长就是 $ A $,$ B $ 两点间的距离. 你同意他们的说法吗?请说明理由.

答案:
【解】同意.
理由:因为$∠DCB=100^{\circ },∠ADC=65^{\circ },$
所以$∠A=180^{\circ }-∠DCB-∠ADC=15^{\circ }.$
又因为$∠BEC=15^{\circ }$,所以$∠A=∠BEC.$
在$△DCA$和$△BCE$中,因为$\left\{\begin{array}{l} ∠A=∠BEC,\\ ∠ACD=∠ECB,\\ CD=BC,\end{array}\right. $
所以$△DCA\cong △BCE(AAS)$,所以$AC=EC.$
又因为$BC=CD$,所以$AC-BC=CE-CD$,即$AB=DE,$
所以测得 DE 的长就是 A,B 两点间的距离.
理由:因为$∠DCB=100^{\circ },∠ADC=65^{\circ },$
所以$∠A=180^{\circ }-∠DCB-∠ADC=15^{\circ }.$
又因为$∠BEC=15^{\circ }$,所以$∠A=∠BEC.$
在$△DCA$和$△BCE$中,因为$\left\{\begin{array}{l} ∠A=∠BEC,\\ ∠ACD=∠ECB,\\ CD=BC,\end{array}\right. $
所以$△DCA\cong △BCE(AAS)$,所以$AC=EC.$
又因为$BC=CD$,所以$AC-BC=CE-CD$,即$AB=DE,$
所以测得 DE 的长就是 A,B 两点间的距离.
10. 新视角 方案设计题 如图,某广场上有一座雕塑,$ A $,$ B $ 两点分别位于其底座两端,但利用现有的皮尺无法直接测出 $ A $,$ B $ 两点间的距离,请你设计一个方案,测出 $ A $,$ B $ 两点间的距离,并说明理由.


答案:
【解】方案:如图,在地面上选择一点 O,连接AO 并延长至点 C,使$OC=OA$,连接 BO 并延长至点 D,使$OD=OB$,连接 CD,测量 CD 的长,CD 的长即为 A,B 两点间的距离.
理由:在$△AOB$和$△COD$中,因为
$\left\{\begin{array}{l} AO=CO,\\ ∠AOB=∠COD,\\ OB=OD,\end{array}\right. $
所以$△AOB\cong △COD(SAS)$,所以$AB=CD.$

【解】方案:如图,在地面上选择一点 O,连接AO 并延长至点 C,使$OC=OA$,连接 BO 并延长至点 D,使$OD=OB$,连接 CD,测量 CD 的长,CD 的长即为 A,B 两点间的距离.
理由:在$△AOB$和$△COD$中,因为
$\left\{\begin{array}{l} AO=CO,\\ ∠AOB=∠COD,\\ OB=OD,\end{array}\right. $
所以$△AOB\cong △COD(SAS)$,所以$AB=CD.$

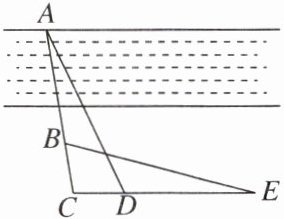
11. 情境题 生活应用 如图,$ AD $ 是一段斜坡,$ AB $ 是水平线,现准备测斜坡上一点 $ D $ 的竖直高度 $ DB $,欢欢在 $ D $ 处立上一根竹竿 $ CD $,并保证 $ CD \perp AD $,然后在竿顶 $ C $ 处垂下一根绳子 $ CE $,与斜坡 $ AD $ 交于点 $ E $,他测出了绳子 $ CE $ 的长度,发现 $ CE = AD $,此时他测得 $ DE = 2 $ 米,求 $ DB $ 的长度.


答案:
【解】如图,延长 CE 交 AB 于点 F,
易知$∠A+∠1=90^{\circ },∠C+∠2=90^{\circ },$
因为$∠1=∠2$,所以$∠A=∠C.$
在$△ABD$和$△CDE$中,$\left\{\begin{array}{l} ∠A=∠C,\\ ∠ABD=∠CDE=90^{\circ },\\ AD=CE,\end{array}\right. $
所以$△ABD\cong △CDE(AAS)$,所以$DB=DE,$
因为$DE=2$米,所以 DB 的长度是 2 米.

【解】如图,延长 CE 交 AB 于点 F,
易知$∠A+∠1=90^{\circ },∠C+∠2=90^{\circ },$
因为$∠1=∠2$,所以$∠A=∠C.$
在$△ABD$和$△CDE$中,$\left\{\begin{array}{l} ∠A=∠C,\\ ∠ABD=∠CDE=90^{\circ },\\ AD=CE,\end{array}\right. $
所以$△ABD\cong △CDE(AAS)$,所以$DB=DE,$
因为$DE=2$米,所以 DB 的长度是 2 米.

查看更多完整答案,请扫码查看


