《2025年学生基础性作业五年级数学上册人教版》

1. 在探索三角形面积的计算方法时,乐乐把三角形转化成了长方形(如图)。若长方形的长为 8 cm,宽为 5 cm,则原三角形的面积是$( )cm^2。$

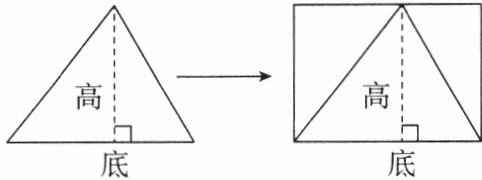
答案： 20

2. 一个平行四边形与一个三角形的底和面积都分别相等。如果三角形的高是 4.8 cm,那么这个平行四边形的高是( )cm。

答案： 2.4

3. 一个大坝的横截面是梯形,这个梯形的上、下底之和是 200 m,面积是$ 3500 m^2,$高是( )m。已知下底的长度是高的 1.5 倍,下底长是( )m。

答案： 35 52.5

4. 把下面四个图形按面积从小到大的顺序排一排。

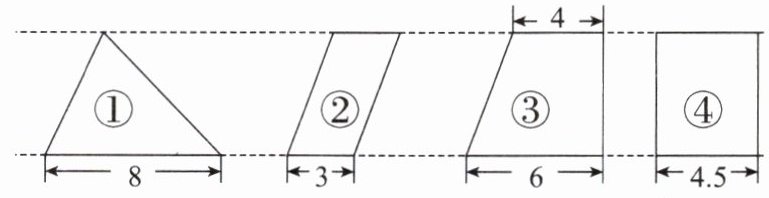
图( )＜ 图( )＜ 图( )＜ 图( )

答案： ② ① ④ ③

5. 从一个上底 5.5 cm,下底 8.5 cm,高 6 cm 的梯形中,剪一个面积最大的平行四边形(其中一组对边在梯形的上、下底边上),这个平行四边形的面积是$( )cm^2,$剩下图形的面积是$( )cm^2。$

答案： 33 9

二、下面是同学们在研究梯形面积时想到的几种方法。

明明( ) 东东( ) 乐乐( ) 红红( )
你觉得谁的方法能推导出梯形的面积公式？在其名字旁边的括号里画“√”。在你认为正确的方法中,你最喜欢谁的方法？请试着把这种方法推导的过程写清楚。

答案： 提示：四种方法都能推导出梯形的面积公式。

三、问题解决。
一个平行四边形,底增加 3 cm 后,面积增加$ 30 cm^2；$高增加 4 cm 后,面积增加$ 48 cm^2。$原平行四边形的面积是多少平方厘米？

答案： 高：30÷3=10（cm），底：48÷4=12（cm），则原平行四边形的面积为10×12=120（cm²）