第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 任意掷一枚六面骰子,掷出来的点数可能是( ),掷出每个点数的可能性( )。
答案:
1,2,3,4,5,6 相同
2. 同时掷三个六面骰子,掷出来的点数之和最大是( ),最小是( )。
答案:
18 3
二、判一判(对的画“√”,错的画“×”)。
1. 同时掷三个六面骰子,掷出来的点数之和可能是 2。( )
2. 同时掷两个六面骰子,掷出来的点数之积可能是 2。( )
3. 同时掷三个六面骰子,掷出来的点数之积可能是 2。( )
4. 同时掷三个六面骰子,掷出来的点数之和可能是 19。( )
1. 同时掷三个六面骰子,掷出来的点数之和可能是 2。( )
2. 同时掷两个六面骰子,掷出来的点数之积可能是 2。( )
3. 同时掷三个六面骰子,掷出来的点数之积可能是 2。( )
4. 同时掷三个六面骰子,掷出来的点数之和可能是 19。( )
答案:
1. × 2. √ 3. √ 4. ×
三、问题解决。
1. 下面是相传的五位著名数学家“掷硬币”的实验数据。
|实验者|掷币次数|正面朝上次数|反面朝上次数|
|德·摩根|4092|2048|2044|
|蒲丰|4040|2048|1992|
|费勒|10000|4979|5021|
|皮尔逊|24000|12012|11988|
|罗曼诺夫斯基|80640|39699|40941|
(1)通过实验发现:掷一枚硬币时,随着实验次数越来越多,正面朝上和反面朝上次数的差距越来越( )(填“大”或“小”)。
(2)掷一枚硬币,正面朝上的可能性和反面朝上的可能性( ),所以在很多球类比赛前,比赛双方采用掷硬币的方式来决定谁开球的规则是( )(填“不公平”或“公平”)的。
(3)两人同时各掷一枚相同的硬币,出现的结果可能是( )、( )、( )或( )。聪聪和乐乐在玩五子棋游戏,他们通过掷两枚相同的硬币来决定谁执黑子,如果朝上的两面相同则聪聪执黑子,否则乐乐执黑子,这一规则公平吗?为什么?
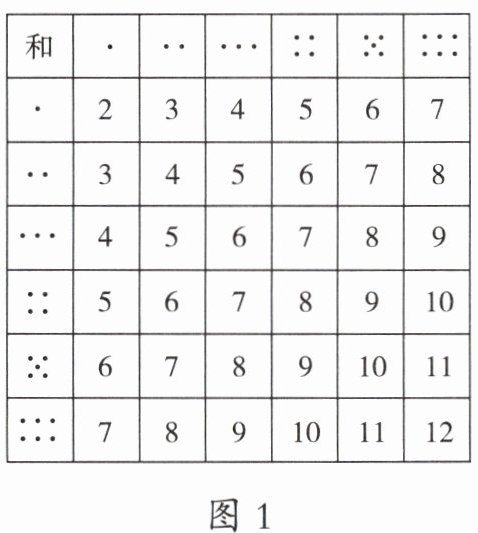
2. 明明和乐乐周末一起玩掷骰子游戏。同时掷出两个骰子,并制作了图 1。
(1)从图 1 中看出,和有( )种不同的结果,分别是( )。
(2)和可能出现 1 或 13 吗?为什么?
(3)将图 1 中和是 5、6、7、8、9 的方格涂色。
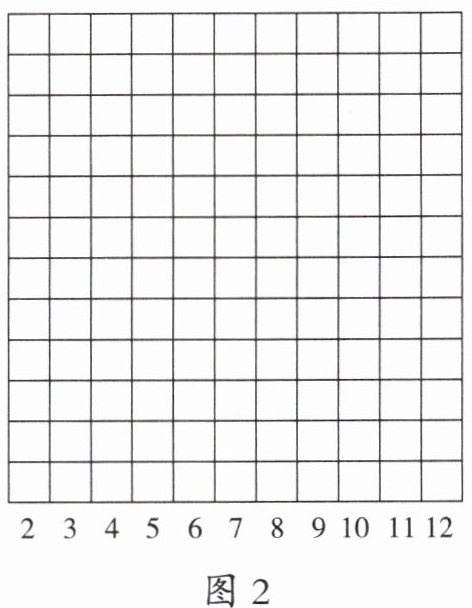
(4)共掷 50 次,结果如下表。和是几,就根据该和出现的次数在图 2 中几的上面涂上对应的格数。
|和|2|3|4|5|6|7|8|9|10|11|12|
|次数|2|3|4|5|8|9|7|5|4|3|0|
从两个图中,你发现了什么?
1. 下面是相传的五位著名数学家“掷硬币”的实验数据。
|实验者|掷币次数|正面朝上次数|反面朝上次数|
|德·摩根|4092|2048|2044|
|蒲丰|4040|2048|1992|
|费勒|10000|4979|5021|
|皮尔逊|24000|12012|11988|
|罗曼诺夫斯基|80640|39699|40941|
(1)通过实验发现:掷一枚硬币时,随着实验次数越来越多,正面朝上和反面朝上次数的差距越来越( )(填“大”或“小”)。
(2)掷一枚硬币,正面朝上的可能性和反面朝上的可能性( ),所以在很多球类比赛前,比赛双方采用掷硬币的方式来决定谁开球的规则是( )(填“不公平”或“公平”)的。
(3)两人同时各掷一枚相同的硬币,出现的结果可能是( )、( )、( )或( )。聪聪和乐乐在玩五子棋游戏,他们通过掷两枚相同的硬币来决定谁执黑子,如果朝上的两面相同则聪聪执黑子,否则乐乐执黑子,这一规则公平吗?为什么?
2. 明明和乐乐周末一起玩掷骰子游戏。同时掷出两个骰子,并制作了图 1。
(1)从图 1 中看出,和有( )种不同的结果,分别是( )。
(2)和可能出现 1 或 13 吗?为什么?
(3)将图 1 中和是 5、6、7、8、9 的方格涂色。


(4)共掷 50 次,结果如下表。和是几,就根据该和出现的次数在图 2 中几的上面涂上对应的格数。
|和|2|3|4|5|6|7|8|9|10|11|12|
|次数|2|3|4|5|8|9|7|5|4|3|0|
从两个图中,你发现了什么?
答案:
1.(1)小 (2)相同 公平 (3)两枚都是正面朝上 两枚都是反面朝上 一枚正面朝上一枚反面朝上 一枚反面朝上一枚正面朝上 公平(理由略) 2.(1)11 2、3、4、5、6、7、8、9、10、11、12 (2)不可能 掷出两枚骰子,每次至少是1,此时和为2;每次最大是6,此时和为12 (3) (4)
(4)  我发现:和在中间的可能性大,在两边的可能性小。(答案合理即可。)
我发现:和在中间的可能性大,在两边的可能性小。(答案合理即可。)
1.(1)小 (2)相同 公平 (3)两枚都是正面朝上 两枚都是反面朝上 一枚正面朝上一枚反面朝上 一枚反面朝上一枚正面朝上 公平(理由略) 2.(1)11 2、3、4、5、6、7、8、9、10、11、12 (2)不可能 掷出两枚骰子,每次至少是1,此时和为2;每次最大是6,此时和为12 (3)
 (4)
(4)  我发现:和在中间的可能性大,在两边的可能性小。(答案合理即可。)
我发现:和在中间的可能性大,在两边的可能性小。(答案合理即可。) 查看更多完整答案,请扫码查看


