第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
一、下面是乐乐和亮亮解答 $4(x + 3) = 32$ 的过程,请仔细观察并回答下面的问题。
| 乐乐的解答: | 亮亮的解答: |
| $4(x + 3) = 32$
解:$4(x + 3) ÷ 4 = 32 ÷ 4$
$x + 3 = 8$
$x + 3 - 3 = 8 - 3$
$x = 5$ | $4(x + 3) = 32$
解:$4x + 12 = 32$
$4x + 12 - 12 = 32 - 12$
$4x = 20$
$x = 5$ |
1. 乐乐的解答过程是先把( )看作一个整体,在等式两边同时( ),把原来复杂的方程转化成简单的方程。
2. 亮亮的解答过程是利用( )律先把括号去掉,把带括号的方程转化成不带括号的方程。
3. 两人解答的过程都用到了( )的数学思想方法。
| 乐乐的解答: | 亮亮的解答: |
| $4(x + 3) = 32$
解:$4(x + 3) ÷ 4 = 32 ÷ 4$
$x + 3 = 8$
$x + 3 - 3 = 8 - 3$
$x = 5$ | $4(x + 3) = 32$
解:$4x + 12 = 32$
$4x + 12 - 12 = 32 - 12$
$4x = 20$
$x = 5$ |
1. 乐乐的解答过程是先把( )看作一个整体,在等式两边同时( ),把原来复杂的方程转化成简单的方程。
2. 亮亮的解答过程是利用( )律先把括号去掉,把带括号的方程转化成不带括号的方程。
3. 两人解答的过程都用到了( )的数学思想方法。
答案:
1. 4(x+3)除以 4 2. 乘法分配 3. 转化
二、解方程。
$2x - 0.9 × 4 = 21.4$ $4x + 1.2 × 5 = 24.4$ $2x + 1.5x = 17.5$
$(x - 0.4) × 2 = 4$ $(3x - 4) × 6 = 48$ $(8x + 0.5) ÷ 1.5 = 11$
$2x - 0.9 × 4 = 21.4$ $4x + 1.2 × 5 = 24.4$ $2x + 1.5x = 17.5$
$(x - 0.4) × 2 = 4$ $(3x - 4) × 6 = 48$ $(8x + 0.5) ÷ 1.5 = 11$
答案:
x=12.5 x=4.6 x=5 x=2.4 x=4 x=2
三、看图列方程,并求出方程的解。
1.
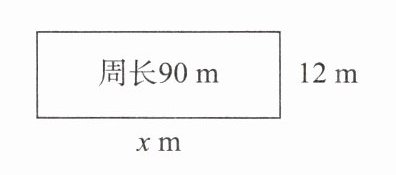
2.

1.

2.

答案:
1.(12+x)×2=90 x=33 2. 25×4+5x=150 x=10
四、求值。
方程 $7x - 11 = 10$ 与 $ax + 3 = 7.5$ 中未知数 $x$ 的解相同,求 $a + 1.5$ 的值。
方程 $7x - 11 = 10$ 与 $ax + 3 = 7.5$ 中未知数 $x$ 的解相同,求 $a + 1.5$ 的值。
答案:
3
查看更多完整答案,请扫码查看


