《2025年家庭作业五年级数学上册人教版》

四、列方程解决问题。
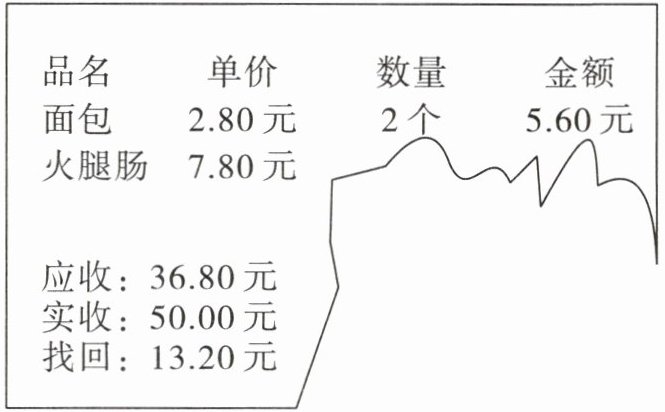
1. 下面是李奶奶在某超市购物结账后的小票,她不小心撕了一部分,请你算一算,李奶奶买了多少根火腿肠？

2. 甲、乙两艘轮船同时从一个码头向相反的方向开出,甲船每小时行26.5km,乙船每小时行25.5km,几小时后两船相距260km？
3. 数学兴趣小组的男生人数是女生人数的3倍,后来有8个男生转到语文兴趣小组,这时数学兴趣小组的男、女生人数一样多。原来数学兴趣小组男、女生各有多少人？
4. 张叔叔和李叔叔住在同一个小区,两家准备去同一景点游玩,两家所走的路线相同。张叔叔开车每小时行驶45km,李叔叔开车每小时行驶60km,张叔叔一家开车2小时后,李叔叔一家才启程,李叔叔一家几小时后追上张叔叔一家？(两家在开车途中的休息时间相同且忽略不计,并假设在追赶过程中张叔叔未到达景点。)

答案： 1.解:设李奶奶买了x根火腿肠。7.80x+5.60=36.80 x=4 2.解:设x小时后两船相距260 km。26.5x+25.5x=260 x=5 3.解:设原来数学兴趣小组的女生有x人,则男生有3x人。3x-8=x x=4 3x=12 4.解:设李叔叔一家x小时后追上张叔叔一家。45×(2+x)=60x x=6

轻松练
$2x + 8x = $$10x$ $9t - t = $$8t$ $7a + a = $$8a$ $12a - 4a = $$8a$
$6.8y - 5.9y = $$0.9y$ $12x + 23x = $$35x$ $3y + 6y - 8y = $$y$ $12a - 7a + 13a = $$18a$

答案： 1. 对于$2x + 8x$：
根据合并同类项法则$ax+bx=(a + b)x$，这里$a = 2$，$b = 8$，则$2x+8x=(2 + 8)x$。
计算$2 + 8=10$，所以$2x + 8x = 10x$。
2. 对于$9t−t$：
把$t$看作$1t$，根据$ax - bx=(a - b)x$，这里$a = 9$，$b = 1$，则$9t−t=(9 - 1)t$。
计算$9−1 = 8$，所以$9t−t = 8t$。
3. 对于$7a + a$：
把$a$看作$1a$，根据$ax+bx=(a + b)x$，这里$a = 7$，$b = 1$，则$7a + a=(7 + 1)a$。
计算$7 + 1=8$，所以$7a + a = 8a$。
4. 对于$12a−4a$：
根据$ax - bx=(a - b)x$，这里$a = 12$，$b = 4$，则$12a−4a=(12 - 4)a$。
计算$12−4 = 8$，所以$12a−4a = 8a$。
5. 对于$6.8y−5.9y$：
根据$ax - bx=(a - b)x$，这里$a = 6.8$，$b = 5.9$，则$6.8y−5.9y=(6.8 - 5.9)y$。
计算$6.8−5.9 = 0.9$，所以$6.8y−5.9y = 0.9y$。
6. 对于$12x + 23x$：
根据$ax+bx=(a + b)x$，这里$a = 12$，$b = 23$，则$12x + 23x=(12 + 23)x$。
计算$12 + 23=35$，所以$12x + 23x = 35x$。
7. 对于$3y+6y−8y$：
先算$3y+6y$，根据$ax+bx=(a + b)x$，$3y+6y=(3 + 6)y=9y$；
再算$9y−8y$，根据$ax - bx=(a - b)x$，$9y−8y=(9 - 8)y$。
计算$9−8 = 1$，所以$3y+6y−8y = y$。
8. 对于$12a−7a+13a$：
先算$12a−7a$，根据$ax - bx=(a - b)x$，$12a−7a=(12 - 7)a = 5a$；
再算$5a+13a$，根据$ax+bx=(a + b)x$，$5a+13a=(5 + 13)a$。
计算$5 + 13=18$，所以$12a−7a+13a = 18a$。
综上，答案依次为：$10x$；$8t$；$8a$；$8a$；$0.9y$；$35x$；$y$；$18a$。