《2025年口算训练六年级数学上册人教版双色升级版》

$8×3.14=$25.12 $28.26÷6.28=$4.5 $C= 12.56cm$ $d=$4cm
$12×3.14=$37.68 $94.2÷3.14=$30 $S= 12.56m^{2}$ $r=$2m
$36×3.14=$113.04 $78.5÷3.14=$25 $S= 314m^{2}$ $r=$10m

答案： 25.12
4.5
4cm
37.68
30
2m
113.04
25
10m

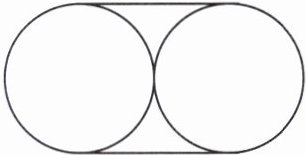
1. 如右图,把两个半径为4cm的圆捆扎在一起,打结处忽略,一共要用掉(41.12)cm长的绳子。

答案： 两个半径为4cm的圆，直径为8cm。
绳子长度由两部分组成：两条直径的长度和一个圆的周长。
两条直径长度：2×8=16cm
一个圆的周长：2×3.14×4=25.12cm
总长度：16+25.12=41.12cm
41.12

2. 在边长为6cm的正方形中画一个最大的圆,圆面积是(28.26)$cm^{2}$。

答案： 圆的直径等于正方形边长，即6cm，半径为6÷2=3cm。
圆面积公式：$S = \pi r^2$
代入得：$S = 3.14×3^2 = 3.14×9 = 28.26$
28.26

3. 一个车轮转2圈,转过的路程是12.56m,车轮半径是(1)m。

答案： 12.56÷2=6.28(m)
6.28÷3.14=2(m)
2÷2=1(m)
1

4. 如果大圆面积是小圆的9倍,那么大圆的直径是小圆的(3)倍。

答案： 设小圆半径为$r$，则小圆面积为$\pi r^2$。
因为大圆面积是小圆的9倍，所以大圆面积为$9\pi r^2$。
设大圆半径为$R$，则$\pi R^2 = 9\pi r^2$，可得$R^2 = 9r^2$，$R = 3r$。
大圆直径为$2R = 6r$，小圆直径为$2r$，所以大圆直径是小圆直径的$6r÷2r = 3$倍。
3

5. $C= 12.56m$,$r= $(2)m,$S= $(12.56)$m^{2}$。

答案： 已知圆的周长$C = 12.56m$，根据圆的周长公式$C=2\pi r$（$\pi$取$3.14$），可得半径$r = C÷(2\pi)=12.56÷(2×3.14)=12.56÷6.28 = 2m$。
再根据圆的面积公式$S=\pi r^{2}$，可得面积$S = 3.14×2^{2}=3.14×4 = 12.56m^{2}$。
$r = 2m$，$S=12.56m^{2}$

6. $S= 78.5cm^{2}$,$r= $(5)cm,$C= $(31.4)cm。

答案： 已知圆的面积$S = 78.5\,\text{cm}^2$，根据圆的面积公式$S=\pi r^2$，可得$r^2=\frac{S}{\pi}=\frac{78.5}{3.14} = 25$，则$r = 5\,\text{cm}$。
根据圆的周长公式$C = 2\pi r$，可得$C=2×3.14×5 = 31.4\,\text{cm}$。
$r = 5$，$C = 31.4$

7. 扇形圆心角的度数是$60^{\circ }$,该扇形的面积是所在圆面积的($\frac{1}{6}$)。

答案： $60^{\circ}÷360^{\circ}=\frac{1}{6}$
$\frac{1}{6}$

8. 一个半径为2cm的半圆,它的周长是(10.28)cm。

答案： 半圆的周长 = 圆周长的一半 + 直径
圆的周长 = 2×π×半径 = 2×3.14×2 = 12.56cm
圆周长的一半 = 12.56÷2 = 6.28cm
直径 = 2×半径 = 2×2 = 4cm
半圆的周长 = 6.28 + 4 = 10.28cm
10.28

1. 扇形的圆心角为$90^{\circ }$,所在圆的半径从2cm增加到4cm,扇形的面积增加了(9.42)$cm^{2}$。

答案： 原来扇形面积：$3.14×2^{2}×\frac{90}{360}=3.14×4×\frac{1}{4}=3.14(cm^{2})$
现在扇形面积：$3.14×4^{2}×\frac{90}{360}=3.14×16×\frac{1}{4}=12.56(cm^{2})$
增加的面积：$12.56 - 3.14 = 9.42(cm^{2})$
9.42

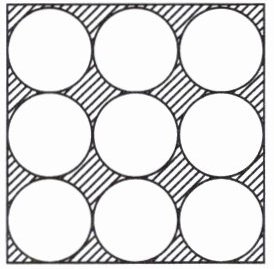
2. 如右图,在边长为6cm的正方形中剪去9个半径为1cm的圆,剩下的面积是(7.74)$cm^{2}$。

答案： 正方形面积：6×6=36(cm²)
一个圆面积：3.14×1²=3.14(cm²)
9个圆面积：3.14×9=28.26(cm²)
剩下面积：36-28.26=7.74(cm²)
7.74