第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
9. 如图所示,灯泡$L_{1}$、$L_{2}$的电阻分别为10Ω、20Ω。闭合开关S,通过$L_{1}$、$L_{2}的电流分别为I_{1}$、$I_{2}$,它们两端的电压分别为$U_{1}$、$U_{2}$,则 (
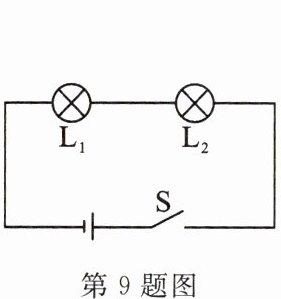
A.$I_{1}:I_{2}= 1:1,U_{1}:U_{2}= 2:1$
B.$I_{1}:I_{2}= 1:2,U_{1}:U_{2}= 1:1$
C.$I_{1}:I_{2}= 1:1,U_{1}:U_{2}= 1:2$
D.$I_{1}:I_{2}= 1:2,U_{1}:U_{2}= 1:2$
C
)
A.$I_{1}:I_{2}= 1:1,U_{1}:U_{2}= 2:1$
B.$I_{1}:I_{2}= 1:2,U_{1}:U_{2}= 1:1$
C.$I_{1}:I_{2}= 1:1,U_{1}:U_{2}= 1:2$
D.$I_{1}:I_{2}= 1:2,U_{1}:U_{2}= 1:2$
答案:
C
10. 如图所示电源电压不变,当开关$S_{1}$闭合、$S_{2}$断开时,电流表的示数为0.4A;当$S_{1}和S_{2}$都闭合时,电流表的示数为1.6A,则电阻$R_{1}与R_{2}$的比值为 (
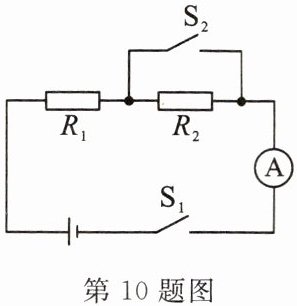
A.1:2
B.2:1
C.1:3
D.3:1
C
)
A.1:2
B.2:1
C.1:3
D.3:1
答案:
C
11. 如图所示,$R_{1}= 12Ω,R_{2}= 4Ω$,将它们串联后接到8V的电源上,则电路的总电阻为
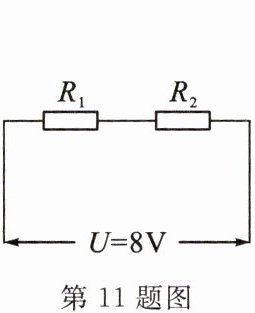
16
Ω,电路中的电流为0.5
A。
答案:
16 0.5
12. 电阻$R_{1}$的U-I图像如图所示,$R_{1}$的阻值是

10
Ω,把$R_{1}$与阻值是30Ω的电阻$R_{2}$串联在电源电压是4V的电路中,通过$R_{1}与R_{2}$的电流之比是$1:1$
,$R_{1}与R_{2}$两端的电压之比是$1:3$
。
答案:
10 $1:1$ $1:3$
13. 如图甲是某电子秤的原理示意图,$R_{1}$为定值电阻,托盘下方的电阻$R_{2}$为压敏电阻,其电阻大小与托盘内所放物体质量m大小的关系如图乙所示,已知电源电压为6V保持不变。
 (1)当托盘为空时,电阻$R_{2}$为
(1)当托盘为空时,电阻$R_{2}$为
(2)闭合开关,若托盘为空时,电流表示数为$I_{1}= 0.01A$,求定值电阻$R_{1}$的阻值。
(3)闭合开关,若放入某物体后,电流表示数为$I_{2}= 0.02A$,求该物体的质量大小。
 (1)当托盘为空时,电阻$R_{2}$为
(1)当托盘为空时,电阻$R_{2}$为500
Ω。(2)闭合开关,若托盘为空时,电流表示数为$I_{1}= 0.01A$,求定值电阻$R_{1}$的阻值。
解:当托盘为空时,电阻 $R_{2}=500\Omega$,电流表示数为 $I_{1}=0.01A$,此时电路中总电阻 $R_{总1}=\frac{U}{I_{1}}=\frac{6V}{0.01A}=600\Omega$,则定值电阻$R_{1}=R_{总1}-R_{2}=600\Omega -500\Omega =100\Omega $
(3)闭合开关,若放入某物体后,电流表示数为$I_{2}= 0.02A$,求该物体的质量大小。
放入某物体后,电流表示数为 $I_{2}=0.02A$,此时电路中总电阻 $R_{总2}=\frac{U}{I_{2}}=\frac{6V}{0.02A}=300\Omega $,则压敏电阻 $R'_{2}=R_{总2}-R_{1}=300\Omega -100\Omega =200\Omega $,由乙图中数据可以得到此时物体质量为 600g
答案:
(1)500
(2)解:当托盘为空时,电阻 $R_{2}=500\Omega$,电流表示数为 $I_{1}=$$0.01A$,此时电路中总电阻 $R_{总1}=$$\frac{U}{I_{1}}=\frac{6V}{0.01A}=600\Omega$,则定值电阻$R_{1}=R_{总1}-R_{2}=600\Omega -500\Omega =$$100\Omega $;
(3)放入某物体后,电流表示数为 $I_{2}=0.02A$,此时电路中总电阻 $R_{总2}=\frac{U}{I_{2}}=\frac{6V}{0.02A}=300\Omega $,则压敏电阻 $R'_{2}=R_{总2}-R_{1}=300\Omega -$$100\Omega =200\Omega $,由乙图中数据可以得到此时物体质量为 600g。
(1)500
(2)解:当托盘为空时,电阻 $R_{2}=500\Omega$,电流表示数为 $I_{1}=$$0.01A$,此时电路中总电阻 $R_{总1}=$$\frac{U}{I_{1}}=\frac{6V}{0.01A}=600\Omega$,则定值电阻$R_{1}=R_{总1}-R_{2}=600\Omega -500\Omega =$$100\Omega $;
(3)放入某物体后,电流表示数为 $I_{2}=0.02A$,此时电路中总电阻 $R_{总2}=\frac{U}{I_{2}}=\frac{6V}{0.02A}=300\Omega $,则压敏电阻 $R'_{2}=R_{总2}-R_{1}=300\Omega -$$100\Omega =200\Omega $,由乙图中数据可以得到此时物体质量为 600g。
14.[科学推理]电阻触摸屏在笔记本电脑及手机等设备上已普遍使用,当手指在触摸屏表面施以一定的压力时,触摸屏通过分别识别触摸点的水平与竖直位置,从而确定触摸的位置。以竖直方向为例,触摸屏相当于一根电阻丝,触摸时,触摸点P将电阻丝分为上下两部分,设上部分电阻为$R_{1}$,下部分电阻为$R_{2}$,结构可等效为如图所示电路,电源电压不变。当触摸点在竖直方向移动时,若测得$R_{2}$两端电压增大,则可知$R_{2}$阻值
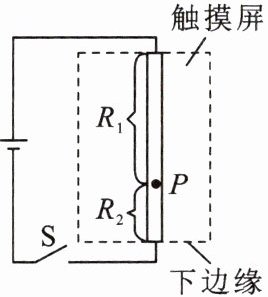
增大
,触摸点P到屏下端的距离增大
。(均选填“增大”“减小”或“不变”)
答案:
增大 增大
查看更多完整答案,请扫码查看


