第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 填一填,算一算。
(1)
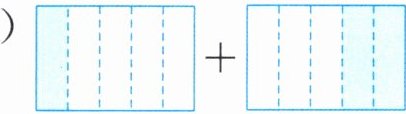
( \ \ \ \ )个$\frac {1}{5}$加上( \ \ \ \ )个$\frac {1}{5}$是( \ \ \ \ )个$\frac {1}{5}$。
$\frac {(\ \ \ \ )}{(\ \ \ \ )}+\frac {(\ \ \ \ )}{(\ \ \ \ )}=\frac {(\ \ \ \ )}{(\ \ \ \ )}$
(2)
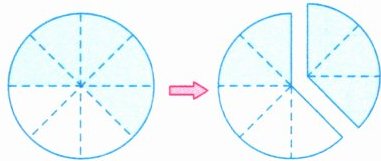
( \ \ \ \ )个$\frac {1}{8}$减去( \ \ \ \ )个$\frac {1}{8}$是( \ \ \ \ )个$\frac {1}{8}$。
$\frac {(\ \ \ \ )}{(\ \ \ \ )}-\frac {(\ \ \ \ )}{(\ \ \ \ )}=\frac {(\ \ \ \ )}{(\ \ \ \ )}$
(1)

( \ \ \ \ )个$\frac {1}{5}$加上( \ \ \ \ )个$\frac {1}{5}$是( \ \ \ \ )个$\frac {1}{5}$。
$\frac {(\ \ \ \ )}{(\ \ \ \ )}+\frac {(\ \ \ \ )}{(\ \ \ \ )}=\frac {(\ \ \ \ )}{(\ \ \ \ )}$
(2)

( \ \ \ \ )个$\frac {1}{8}$减去( \ \ \ \ )个$\frac {1}{8}$是( \ \ \ \ )个$\frac {1}{8}$。
$\frac {(\ \ \ \ )}{(\ \ \ \ )}-\frac {(\ \ \ \ )}{(\ \ \ \ )}=\frac {(\ \ \ \ )}{(\ \ \ \ )}$
答案:
1.
(1)1 2 3 $\frac{1}{5} + \frac{2}{5} = \frac{3}{5}$
(2)5 3 2 $\frac{5}{8} - \frac{3}{8} = \frac{2}{8}$
(1)1 2 3 $\frac{1}{5} + \frac{2}{5} = \frac{3}{5}$
(2)5 3 2 $\frac{5}{8} - \frac{3}{8} = \frac{2}{8}$
2. 直接写出得数。
$\frac {1}{9}+\frac {2}{9}=$ $\frac {6}{10}+\frac {3}{10}=$
$\frac {3}{4}-\frac {1}{4}=$ $\frac {1}{8}+\frac {4}{8}=$
$\frac {4}{5}-\frac {1}{5}=$ $\frac {6}{7}-\frac {5}{7}=$
$\frac {1}{9}+\frac {2}{9}=$ $\frac {6}{10}+\frac {3}{10}=$
$\frac {3}{4}-\frac {1}{4}=$ $\frac {1}{8}+\frac {4}{8}=$
$\frac {4}{5}-\frac {1}{5}=$ $\frac {6}{7}-\frac {5}{7}=$
答案:
2.$\frac{3}{9} \frac{9}{10} \frac{2}{4} \frac{5}{8} \frac{3}{5} \frac{1}{7}$
3. (金华真题)请你接着涂,使涂色部分占整个长方形的$\frac {7}{9}$,并根据涂色过程,写出一个分数加法算式。


答案:
3.![img alt=图片3] $\frac{1}{9} + \frac{6}{9} = \frac{7}{9}$
4. (地域美食)下面是张师傅制作东坡肉时用到的各种调料占调料总量的情况。

(1) 用到的冰糖和料酒一共占调料总量的$\frac {(\ \ \ \ )}{(\ \ \ \ )}$。
(2) 若用到的老抽比冰糖少占调料总量的$\frac {1}{7}$,则生抽和老抽相比,哪种用得多?多占调料总量的几分之几?

(1) 用到的冰糖和料酒一共占调料总量的$\frac {(\ \ \ \ )}{(\ \ \ \ )}$。
(2) 若用到的老抽比冰糖少占调料总量的$\frac {1}{7}$,则生抽和老抽相比,哪种用得多?多占调料总量的几分之几?
答案:
4.
(1)$\frac{3}{7}$
(2)$\frac{2}{7} - \frac{1}{7} = \frac{1}{7} \quad \frac{1}{7} < \frac{3}{7}$
$\frac{3}{7} - \frac{1}{7} = \frac{2}{7}$ 生抽用得多,多占调料总量的$\frac{2}{7}$
(1)$\frac{3}{7}$
(2)$\frac{2}{7} - \frac{1}{7} = \frac{1}{7} \quad \frac{1}{7} < \frac{3}{7}$
$\frac{3}{7} - \frac{1}{7} = \frac{2}{7}$ 生抽用得多,多占调料总量的$\frac{2}{7}$
5. (易错题)妈妈买了一盒点心,欣欣吃了$\frac {4}{7}$,比妹妹多吃了这盒点心的$\frac {2}{7}$。她们一共吃了这盒点心的几分之几?
答案:
5.$\frac{4}{7} - \frac{2}{7} = \frac{2}{7} \quad \frac{2}{7} + \frac{4}{7} = \frac{6}{7}$
易错分析:易直接将题干中出现的两个分数相加。本题应该先算出妹妹吃了这盒点心的几分之几,再将两人吃的量合起来。
易错分析:易直接将题干中出现的两个分数相加。本题应该先算出妹妹吃了这盒点心的几分之几,再将两人吃的量合起来。
6. 一瓶牛奶,爸爸喝了$\frac {2}{7}$,妈妈喝了$\frac {3}{7}$,这瓶牛奶比原来少了几分之几?
答案:
6.$\frac{2}{7} + \frac{3}{7} = \frac{5}{7}$ 解析:这瓶牛奶比原来少的部分就是爸爸、妈妈喝了的部分之和。
查看更多完整答案,请扫码查看


