《2025年阳光同学计算小达人六年级数学上册苏教版》

数形结合 如图,芳芳在长方体盒子里摆了若干个棱长为1厘米的小正方体。

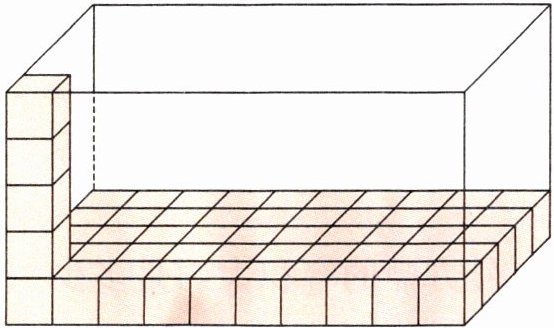
(1)这个长方体盒子的体积是多少立方分米？(不考虑盒子的厚度)
(2)在保证能准确地算出这个长方体盒子的体积的前提下,芳芳最多还能去掉多少个小正方体？

答案：
(1)10×5×5=250(立方厘米) 250立方厘米=0.25立方分米
(2)(10-1)×(5-1)=36(个)

1. 新题型 一个学习小组的四名同学观察并测量了一个长方体。这四名同学得到的数据都是正确的。
甲说：“如果高再增加2分米,那么它恰好是一个正方体。”( )
乙说：“长方体的前后左右四个面的面积之和是96平方分米。”( )
丙说：“它的底面周长是24分米。”( )
丁说：“这个长方体的棱长总和是64分米。”( )
选择哪几个条件可以求出长方体的体积？在对应条件右边的括号里画“√”,并求出这个长方体的体积。

答案： 示例:甲(√) 乙( ) 丙(√) 丁( )
长、宽:24÷4=6(分米)
高:6-2=4(分米)
体积:6×6×4=144(立方分米)