《2025年假期超车道八年级数学》

15. 如图,在Rt△ABC中,∠C= 90°,AC= 8,BC= 6,D为AC上一点,若BD是∠ABC的平分线,则AD= ______.

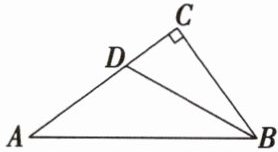
答案： 5

16. 有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺. 如果把这根芦苇拉向水池一边的中点,那么它的顶端恰好到达池边的水面. 水的深度是______尺.(尺是长度单位,1尺= $\frac{1}{3}$m.)

答案： 12

17. 现有三块两直角边长分别为1和2的直角三角形纸板,借助下面5×5的网格,用全部纸板分别拼出3个面积为3且周长不同的四边形,并写出相应四边形的周长.

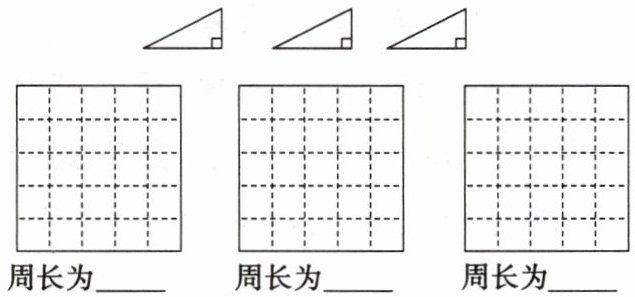
答案：
解：如图所示。
　　　　　　
　　　　

18. “儿童散学归来早,忙趁东风放纸鸢.”又到了放风筝的最佳时节,松松在学习了“勾股定理”之后,为了计算如图所示的风筝的垂直高度CE,他测得以下数据：

①水平距离BD的长为8m；②由手中剩余线的长度得出风筝线BC的长为17m；③牵线放风筝的松松的身高为1.6m.
求风筝的垂直高度CE.

答案： 解：在Rt△CDB中，
　由勾股定理得，CD²=BC²−BD²=17²−8²=225。
∵CD＞0，
∴CD=15。
∴CE=CD+DE=15+1.6=16.6。
　答：风筝的垂直高度CE为16.6m。

19. 已知△ABC的边长a= $n^{2}-1$,b= 2n,c= $n^{2}+1$,且n＞1.
(1)判断三角形的形状,并说明理由；
(2)若∠B= 60°,求△ABC的三边长.

答案： 解：
(1)△ABC是直角三角形，理由如下：
∵a=n²−1，b=2n，c=n²+1，
∴a²+b²=(n²−1)²+(2n)²=n⁴−2n²+1+4n²=n⁴+2n²+1=(n²+1)²，c²=(n²+1)²。
∴a²+b²=c²。
∴△ABC是直角三角形，且∠C=90°。
(2)
∵∠B=60°，∠C=90°，
∴∠A=30°。
∴c=2a，即n²+1=2(n²−1)。
∴n²=3。
　解得n=$\sqrt{3}$或n=−$\sqrt{3}$(不符合题意，舍去)。
　当n=$\sqrt{3}$时，a=n²−1=($\sqrt{3}$)²−1=3−1=2，b=2n=2$\sqrt{3}$，c=2a=4。