第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
[解题策略] 方差是反映一组数据波动大小的一个量。方差越大,则这组数据的波动程度越大;反之,则这组数据的波动程度越小,稳定性越好。结合实际,利用方差的含义,作出决策。
例2 某校开展航天知识竞赛活动。经过几轮筛选,八(2)班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差如下表:
| | 甲 | 乙 | 丙 | 丁 |
| 平均数 | 96 | 98 | 95 | 98 |
| 方差 | 2 | 0.4 | 0.4 | 1.6 |
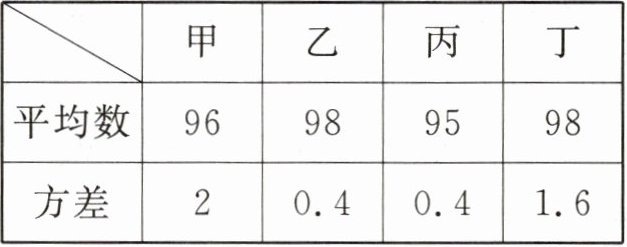
如果要选一名成绩好且状态稳定的同学参赛,那么应该选择 ( )
A.甲
B.乙
C.丙
D.丁
[思路点拨] 根据方差作决策,解题的关键是掌握方差及平均数的意义和计算公式,再具体问题具体分析。
[答案] B
例2 某校开展航天知识竞赛活动。经过几轮筛选,八(2)班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差如下表:
| | 甲 | 乙 | 丙 | 丁 |
| 平均数 | 96 | 98 | 95 | 98 |
| 方差 | 2 | 0.4 | 0.4 | 1.6 |

如果要选一名成绩好且状态稳定的同学参赛,那么应该选择 ( )
A.甲
B.乙
C.丙
D.丁
[思路点拨] 根据方差作决策,解题的关键是掌握方差及平均数的意义和计算公式,再具体问题具体分析。
[答案] B
答案:
B
[解题策略] 本章中构建方程模型主要利用了平均数、中位数、众数的概念,将一组数据中的未知数据用字母表示,然后根据公式或定义列出方程(或方程组),求出数据中的未知数据,从而解决问题。
例3 若一组数据1,2,4,3,x,0的平均数是2,则众数是 ( )
A.1
B.2
C.3
D.4
[思路点拨] 根据平均数的定义,先求出x,然后根据众数的定义解答即可。
[答案] B
例3 若一组数据1,2,4,3,x,0的平均数是2,则众数是 ( )
A.1
B.2
C.3
D.4
[思路点拨] 根据平均数的定义,先求出x,然后根据众数的定义解答即可。
[答案] B
答案:
B
[解题策略] 熟知平均数、中位数、众数、方差的计算方式和优缺点,明确平均数、中位数、众数是描述一组数据的集中趋势的统计量,方差刻画一组数据的离散程度等,然后根据它们的实际意义和题目要求选择适当的统计量进行分析。
例4 某市在实施居民用水定额管理前,对居民的生活用水情况进行了调查。通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如下表:
| 序号 | 月均用水量/t |
| 1 | 1.3 |
| 2 | 1.3 |
…| $$… | $$ |
| 25 | 4.5 |
| 26 | 4.5 |
…| $$… | $$ |
| 50 | 6.4 |
| 51 | 6.8 |
…| $$… | $$ |
| 75 | 11 |
| 76 | 13 |
…| $$… | $$ |
| 99 | 25.6 |
| 100 | 28 |
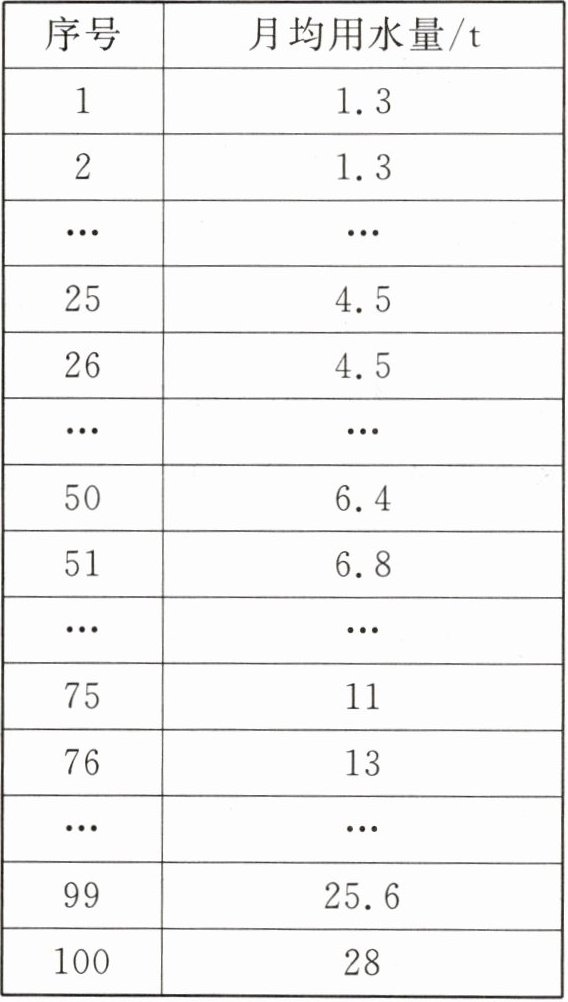
(1)求这组数据的中位数。已知这组数据的平均数为9.2,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费。若要使75%的家庭水费支出不受影响,则这个标准应该定为多少?
[思路点拨] 平均数是表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据的波动程度。
[解] (1)共有100个数,按从小到大的顺序排列后第50,51个数据分别是6.4,6.8,所以中位数为$(6.4 + 6.8)÷2 = 6.6$。
∵这组数据的平均数为9.2,
∴从平均数与中位数的差异可得大部分居民家庭去年的月均用水量小于平均数,有节约用水观念,少数家庭用水比较浪费。
答:这组数据的中位数是6.6。
(2)∵$100×75\% = 75$,
第75个家庭去年的月均用水量为11t,
∴为了鼓励节约用水,要使75%的家庭水费支出不受影响,即要使75户的家庭水费支出不受影响,故家庭月均用水量应该定为11t。
答:这个标准应该定为11t。
例4 某市在实施居民用水定额管理前,对居民的生活用水情况进行了调查。通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如下表:
| 序号 | 月均用水量/t |
| 1 | 1.3 |
| 2 | 1.3 |
…| $$… | $$ |
| 25 | 4.5 |
| 26 | 4.5 |
…| $$… | $$ |
| 50 | 6.4 |
| 51 | 6.8 |
…| $$… | $$ |
| 75 | 11 |
| 76 | 13 |
…| $$… | $$ |
| 99 | 25.6 |
| 100 | 28 |

(1)求这组数据的中位数。已知这组数据的平均数为9.2,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费。若要使75%的家庭水费支出不受影响,则这个标准应该定为多少?
[思路点拨] 平均数是表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据的波动程度。
[解] (1)共有100个数,按从小到大的顺序排列后第50,51个数据分别是6.4,6.8,所以中位数为$(6.4 + 6.8)÷2 = 6.6$。
∵这组数据的平均数为9.2,
∴从平均数与中位数的差异可得大部分居民家庭去年的月均用水量小于平均数,有节约用水观念,少数家庭用水比较浪费。
答:这组数据的中位数是6.6。
(2)∵$100×75\% = 75$,
第75个家庭去年的月均用水量为11t,
∴为了鼓励节约用水,要使75%的家庭水费支出不受影响,即要使75户的家庭水费支出不受影响,故家庭月均用水量应该定为11t。
答:这个标准应该定为11t。
答案:
(1)6.6;
(2)11
(1)6.6;
(2)11
查看更多完整答案,请扫码查看


