第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
11. 已知f(x) = 3x,则f(1) = ______。
答案:
3
12. 已知直线y = kx + b过第一象限且函数值随着x的增大而减小,请列举出来这样的一条直线:______。
答案:
y=-2x+1(答案不唯一,满足k<0,b>0即可)
13. 如图,直线$y_1 = k_1x$与直线$y_2 = k_2x + b$相交于点A(1,2)。当$y_1 < y_2$时,x的取值范围是______。
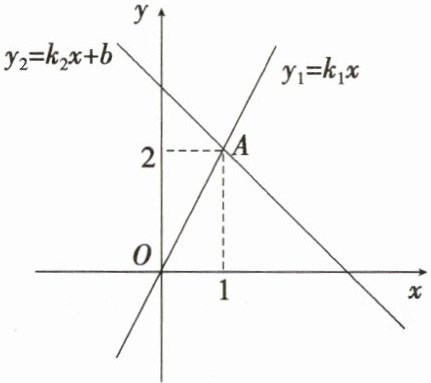

答案:
x<1
14. 如图所示是一个运算程序示意图,若开始输入x的值是3,则输出y的值是______。


答案:
2
15. 一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分时,再打开出水管排水,8分时,关闭进水管,直至容器中的水全部排完。在整个过程中,容器中的水量y(升)与时间x(分)之间的函数关系如图所示,则图中a的值是______。
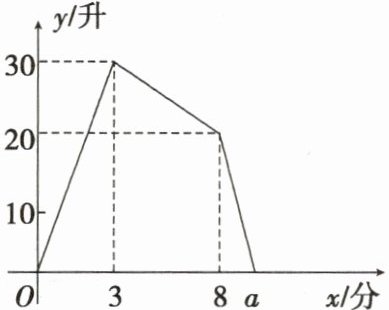

答案:
$\dfrac{29}{3}$
16. 如图,一次函数y = x + 4与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC = 45°,PC = PO,则点P的坐标是______。


答案:
$(-2\sqrt{2},4-2\sqrt{2})$
17. 如图,直线y = $\frac{1}{2}$x + 1与x轴交于点A,点A关于y轴的对称点为A',设经过点A'和y轴上的点B(0,2)的直线为y = kx + b。
(1)求点A'的坐标;
(2)确定直线A'B对应的函数表达式。
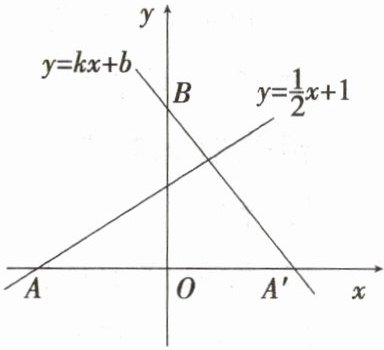
(1)求点A'的坐标;
(2)确定直线A'B对应的函数表达式。

答案:
解:
(1)令y=0,则$\dfrac{1}{2}x+1=0,$
∴x=-2.
∴点A的坐标为(-2,0).
∵点A关于y轴的对称点为A',
∴点A'的坐标为(2,0).
(2)设直线A'B的函数表达式为y=kx+b,
∴$\begin{cases}2k+b=0, \\b=2. \end{cases}$解得$\begin{cases}k=-1, \\b=2. \end{cases}$
∴直线A'B对应的函数表达式为y=-x+2.
(1)令y=0,则$\dfrac{1}{2}x+1=0,$
∴x=-2.
∴点A的坐标为(-2,0).
∵点A关于y轴的对称点为A',
∴点A'的坐标为(2,0).
(2)设直线A'B的函数表达式为y=kx+b,
∴$\begin{cases}2k+b=0, \\b=2. \end{cases}$解得$\begin{cases}k=-1, \\b=2. \end{cases}$
∴直线A'B对应的函数表达式为y=-x+2.
查看更多完整答案,请扫码查看


