第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
7. 女子 10 千米越野滑雪比赛中,甲、乙两位选手同时出发后离起点的距离 y(千米)与时间 t(分)之间的函数关系如图所示,则甲比乙提前______分钟到达终点.


答案:
1
8. 物理实验证实:在弹性限度内,某弹簧长度 y(cm)与所挂物体质量 x(kg)满足函数关系$y = kx + 15$. 下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
| x/kg | 0 | 2 | 5 |
| y/cm | 15 | 19 | 25 |
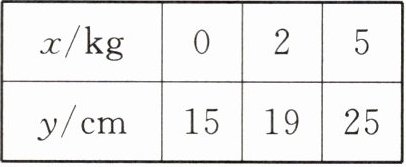
(1)求 y 与 x 的函数关系式;
(2)当弹簧长度为 20 cm 时,求所挂物体的质量.
| x/kg | 0 | 2 | 5 |
| y/cm | 15 | 19 | 25 |

(1)求 y 与 x 的函数关系式;
(2)当弹簧长度为 20 cm 时,求所挂物体的质量.
答案:
解:
(1)把x=2,y=19代入y=kx+15中,
得19=2k+15,解得k=2.
所以y与x的函数关系式为y=2x+15(x≥0).
(2)把y=20代入y=2x+15中,
得20=2x+15,解得x=2.5.
所以所挂物体的质量为2.5 kg.
(1)把x=2,y=19代入y=kx+15中,
得19=2k+15,解得k=2.
所以y与x的函数关系式为y=2x+15(x≥0).
(2)把y=20代入y=2x+15中,
得20=2x+15,解得x=2.5.
所以所挂物体的质量为2.5 kg.
9. 某运输公司安排甲、乙两种货车 24 辆恰好一次性将 328 吨的物资运往 A,B 两地,两种货车载质量及到 A,B 两地的运输成本如下表:
| 货车类型 | 载质量/(吨/辆) | 运往 A 地的成本/(元/辆) | 运往 B 地的成本/(元/辆) |
| 甲种 | 16 | 1 200 | 900 |
| 乙种 | 12 | 1 000 | 750 |
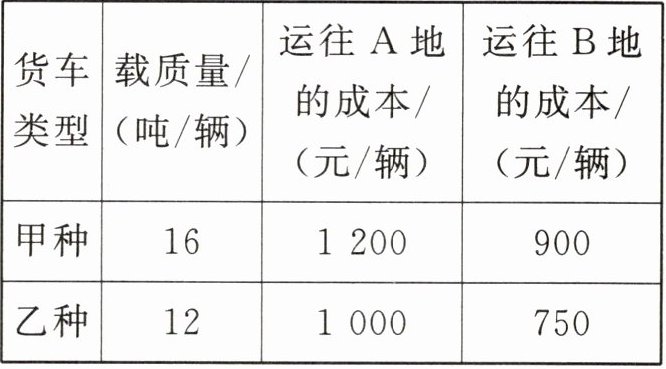
(1)求甲、乙两种货车各用了多少辆.
(2)如果前往 A 地的甲、乙两种货车共 12 辆,所运物资不少于 160 吨,其余货车将剩余物资运往 B 地. 设甲、乙两种货车到 A,B 两地的总运输成本为 w 元,前往 A 地的甲种货车为 t 辆.
①写出 w 与 t 之间的函数解析式.
②当 t 为何值时,w 最小? 最小值是多少?
| 货车类型 | 载质量/(吨/辆) | 运往 A 地的成本/(元/辆) | 运往 B 地的成本/(元/辆) |
| 甲种 | 16 | 1 200 | 900 |
| 乙种 | 12 | 1 000 | 750 |

(1)求甲、乙两种货车各用了多少辆.
(2)如果前往 A 地的甲、乙两种货车共 12 辆,所运物资不少于 160 吨,其余货车将剩余物资运往 B 地. 设甲、乙两种货车到 A,B 两地的总运输成本为 w 元,前往 A 地的甲种货车为 t 辆.
①写出 w 与 t 之间的函数解析式.
②当 t 为何值时,w 最小? 最小值是多少?
答案:
解:
(1)设甲种货车用了x辆,则乙种货车用了(24-x)辆.
根据题意,得16x+12(24-x)=328,
解得x=10,
∴24-x=24-10=14.
答:甲种货车用了10辆,乙种货车用了14辆.
(2)①根据题意,得
w=1 200t+1 000(12-t)+900(10-t)+750[14-(12-t)]=50t+22 500.
∴w与t之间的函数解析式是w=50t+22 500.②
∵t≥0,
12-t≥0,
10-t≥0,
14-(12-t)≥0,
∴0≤t≤10.
∵前往A地的甲、乙两种货车共12辆,所运物资不少于160吨,
∴16t+12(12-t)≥160,
解得t≥4.
∴4≤t≤10.
在w=50t+22 500中,
∵50>0,
∴w随t的增大而增大.
∴t=4时,w最小,最小值是50×4+22 500=22 700(元).
答:当t为4时,w最小,最小值是22 700元.
(1)设甲种货车用了x辆,则乙种货车用了(24-x)辆.
根据题意,得16x+12(24-x)=328,
解得x=10,
∴24-x=24-10=14.
答:甲种货车用了10辆,乙种货车用了14辆.
(2)①根据题意,得
w=1 200t+1 000(12-t)+900(10-t)+750[14-(12-t)]=50t+22 500.
∴w与t之间的函数解析式是w=50t+22 500.②
∵t≥0,
12-t≥0,
10-t≥0,
14-(12-t)≥0,
∴0≤t≤10.
∵前往A地的甲、乙两种货车共12辆,所运物资不少于160吨,
∴16t+12(12-t)≥160,
解得t≥4.
∴4≤t≤10.
在w=50t+22 500中,
∵50>0,
∴w随t的增大而增大.
∴t=4时,w最小,最小值是50×4+22 500=22 700(元).
答:当t为4时,w最小,最小值是22 700元.
10. 某企业下属 A,B 两厂向甲、乙两地运送水泥共 520 吨,A 厂比 B 厂少运送 20 吨,从 A 厂运往甲、乙两地的运费分别为 40 元/吨和 35 元/吨,从 B 厂运往甲、乙两地的运费分别为 28 元/吨和 25 元/吨.
(1)A,B 两厂各运送多少吨水泥?
(2)现甲地需要水泥 240 吨,乙地需要水泥 280 吨. 受条件限制,B 厂运往甲地的水泥最多 150 吨. 设从 A 厂运往甲地 a 吨水泥,A,B 两厂运往甲、乙两地的总运费为 w 元. 求 w 与 a 之间的函数关系式,请你为该企业设计一种总运费最低的运输方案,并说明理由.
(1)A,B 两厂各运送多少吨水泥?
(2)现甲地需要水泥 240 吨,乙地需要水泥 280 吨. 受条件限制,B 厂运往甲地的水泥最多 150 吨. 设从 A 厂运往甲地 a 吨水泥,A,B 两厂运往甲、乙两地的总运费为 w 元. 求 w 与 a 之间的函数关系式,请你为该企业设计一种总运费最低的运输方案,并说明理由.
答案:
解:
(1)设A厂运送水泥x吨,则B厂运送水泥(x+20)吨.
根据题意,得x+x+20=520,解得x=250.
此时,x+20=250+20=270.
答:A厂运送水泥250吨,B厂运送水泥270吨.
(2)设从A厂运往甲地水泥a吨,则A厂运往乙地水泥(250-a)吨,B厂运往甲地水泥(240-a)吨,B厂运往乙地水泥280-(250-a)=(30+a)吨.
由题意,得w=40a+35(250-a)+28(240-a)+25(a+30)=40a+8 750-35a+6 720-28a+25a+750=2a+16 220.
∵B厂运往甲地的水泥最多150吨,
∴240-a≤150,解得a≥90.
∵2>0,
∴w随a值的增大而增大.
∴当a=90时,总运费最低,w最低=2×90+16 220=16 400(元).
∴总运费最低的运送方案为A厂运往甲地水泥90(吨),A厂运往乙地水泥250-90=160(吨);B厂运往甲地水泥150(吨),B厂运往乙地水泥90+30=120(吨),最低运费为16 400元.
(1)设A厂运送水泥x吨,则B厂运送水泥(x+20)吨.
根据题意,得x+x+20=520,解得x=250.
此时,x+20=250+20=270.
答:A厂运送水泥250吨,B厂运送水泥270吨.
(2)设从A厂运往甲地水泥a吨,则A厂运往乙地水泥(250-a)吨,B厂运往甲地水泥(240-a)吨,B厂运往乙地水泥280-(250-a)=(30+a)吨.
由题意,得w=40a+35(250-a)+28(240-a)+25(a+30)=40a+8 750-35a+6 720-28a+25a+750=2a+16 220.
∵B厂运往甲地的水泥最多150吨,
∴240-a≤150,解得a≥90.
∵2>0,
∴w随a值的增大而增大.
∴当a=90时,总运费最低,w最低=2×90+16 220=16 400(元).
∴总运费最低的运送方案为A厂运往甲地水泥90(吨),A厂运往乙地水泥250-90=160(吨);B厂运往甲地水泥150(吨),B厂运往乙地水泥90+30=120(吨),最低运费为16 400元.
查看更多完整答案,请扫码查看


