第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
19. 计算:
(1)$\sqrt {48}÷\sqrt {3}-\sqrt {\frac {1}{2}}×\sqrt {12}+\sqrt {24}$;
(2)$(2\sqrt {5}+\sqrt {3})^{2}-(\sqrt {5}+\sqrt {2})(\sqrt {5}-\sqrt {2})$.
(1)$\sqrt {48}÷\sqrt {3}-\sqrt {\frac {1}{2}}×\sqrt {12}+\sqrt {24}$;
(2)$(2\sqrt {5}+\sqrt {3})^{2}-(\sqrt {5}+\sqrt {2})(\sqrt {5}-\sqrt {2})$.
答案:
(1)原式$=\sqrt{48÷ 3}-\sqrt{\frac{1}{2}× 12}+2\sqrt{6}$$=4-\sqrt{6}+2\sqrt{6}=4+\sqrt{6}$.
(2)原式$=20+4\sqrt{15}+3-(5-2)=20+4\sqrt{15}$.
(1)原式$=\sqrt{48÷ 3}-\sqrt{\frac{1}{2}× 12}+2\sqrt{6}$$=4-\sqrt{6}+2\sqrt{6}=4+\sqrt{6}$.
(2)原式$=20+4\sqrt{15}+3-(5-2)=20+4\sqrt{15}$.
20. 在一条东西走向的河流一侧有一村庄 C,河边原有两个取水点 A,B,其中$AB= AC$,由于某种原因,由 C 到 A 的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点 D(A,D,B 在同一条直线上),并新修一条路 CD,测得$CB= 6.5$千米,$CD= 6$千米,$BD= 2.5$千米.
(1) 求证:$CD⊥AB$;
(2) 求原来的路线 AC 的长.

(1) 求证:$CD⊥AB$;
(2) 求原来的路线 AC 的长.

答案:
(1)$\because CB=6.5$千米,$CD=6$千米,$BD=2.5$千米,$6^{2}+2.5^{2}=6.5^{2}$,$\therefore CD^{2}+BD^{2}=CB^{2}$.$\therefore \triangle CDB$为直角三角形.$\therefore CD\perp AB$.
(2)设$AC=x$千米,则$AB=AC=x$千米,$AD=(x-2.5)$千米.$\because CD\perp AB$,$\therefore \angle ADC=90^{\circ}$.$\therefore CD^{2}+AD^{2}=AC^{2}$,即$6^{2}+(x-2.5)^{2}=x^{2}$.解得$x=8.45$.答:原来的路线$AC$的长为8.45千米.
(1)$\because CB=6.5$千米,$CD=6$千米,$BD=2.5$千米,$6^{2}+2.5^{2}=6.5^{2}$,$\therefore CD^{2}+BD^{2}=CB^{2}$.$\therefore \triangle CDB$为直角三角形.$\therefore CD\perp AB$.
(2)设$AC=x$千米,则$AB=AC=x$千米,$AD=(x-2.5)$千米.$\because CD\perp AB$,$\therefore \angle ADC=90^{\circ}$.$\therefore CD^{2}+AD^{2}=AC^{2}$,即$6^{2}+(x-2.5)^{2}=x^{2}$.解得$x=8.45$.答:原来的路线$AC$的长为8.45千米.
21. 如图,已知四边形 ABCD 是平行四边形,其对角线相交于点 O,$OA= 3$,$BD= 8$,$AB= 5$.
(1)$△AOB$是直角三角形吗?请说明理由.
(2) 求证:四边形 ABCD 是菱形.

(1)$△AOB$是直角三角形吗?请说明理由.
(2) 求证:四边形 ABCD 是菱形.

答案:
(1)解:$\triangle AOB$是直角三角形.理由如下:$\because$四边形$ABCD$是平行四边形,$BD=8$,$\therefore OB=OD=\frac{1}{2}BD=4$.$\because OA=3$,$OB=4$,$AB=5$,$\therefore OA^{2}+OB^{2}=AB^{2}$.$\therefore \triangle AOB$是直角三角形,且$\angle AOB=90^{\circ}$.
(2)证明:由
(1)可知,$\angle AOB=90^{\circ}$,$\therefore AC\perp BD$.$\therefore$平行四边形$ABCD$是菱形.
(1)解:$\triangle AOB$是直角三角形.理由如下:$\because$四边形$ABCD$是平行四边形,$BD=8$,$\therefore OB=OD=\frac{1}{2}BD=4$.$\because OA=3$,$OB=4$,$AB=5$,$\therefore OA^{2}+OB^{2}=AB^{2}$.$\therefore \triangle AOB$是直角三角形,且$\angle AOB=90^{\circ}$.
(2)证明:由
(1)可知,$\angle AOB=90^{\circ}$,$\therefore AC\perp BD$.$\therefore$平行四边形$ABCD$是菱形.
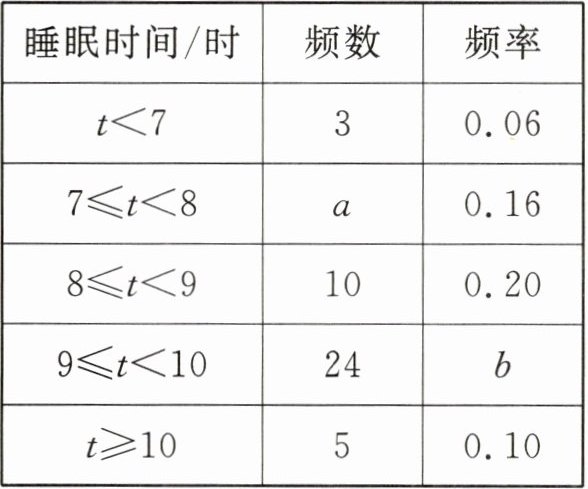
22. 某校数学社团成员采用随机抽样的方法,抽取了八年级部分学生,对他们一周内平均每天的睡眠时间 t(单位:时)进行了调查,将数据整理后得到下列统计表(不完整):
|睡眠时间/时|频数|频率|
|$t<7$|3|0.06|
|$7≤t<8$|a|0.16|
|$8≤t<9$|10|0.20|
|$9≤t<10$|24|b|
|$t≥10$|5|0.10|
请根据统计表中的信息回答下列问题:
(1)$a= $____,$b= $____.
(2) 请估计该校 600 名八年级学生中平均每天的睡眠时间不足 9 小时的人数.
(3) 研究表明,中学生每天睡眠时间低于 9 小时,会影响学习效率. 请你根据以上调查统计结果,向学校提出一条合理化的建议.
|睡眠时间/时|频数|频率|
|$t<7$|3|0.06|
|$7≤t<8$|a|0.16|
|$8≤t<9$|10|0.20|
|$9≤t<10$|24|b|
|$t≥10$|5|0.10|

请根据统计表中的信息回答下列问题:
(1)$a= $____,$b= $____.
(2) 请估计该校 600 名八年级学生中平均每天的睡眠时间不足 9 小时的人数.
(3) 研究表明,中学生每天睡眠时间低于 9 小时,会影响学习效率. 请你根据以上调查统计结果,向学校提出一条合理化的建议.
答案:
(1)本次抽取的学生有:$3÷ 0.06=50$(人).$a=50× 0.16=8$,$b=24÷ 50=0.48$.故答案为:8,0.48.
(2)$600× (0.06+0.16+0.20)=600× 0.42=252$(人).答:估计该校600名八年级学生中平均每天的睡眠时间不足9小时的有252人.
(3)根据表格中的数据可知,有接近一半的学生睡眠时间不足9小时,给学校的建议是:近期组织一次家长会,就学生们的睡眠时间进行强调,要求家长监管好孩子们的睡眠时间,要不少于9小时.(合理即可)
(1)本次抽取的学生有:$3÷ 0.06=50$(人).$a=50× 0.16=8$,$b=24÷ 50=0.48$.故答案为:8,0.48.
(2)$600× (0.06+0.16+0.20)=600× 0.42=252$(人).答:估计该校600名八年级学生中平均每天的睡眠时间不足9小时的有252人.
(3)根据表格中的数据可知,有接近一半的学生睡眠时间不足9小时,给学校的建议是:近期组织一次家长会,就学生们的睡眠时间进行强调,要求家长监管好孩子们的睡眠时间,要不少于9小时.(合理即可)
查看更多完整答案,请扫码查看


