《2025年假期超车道八年级数学》

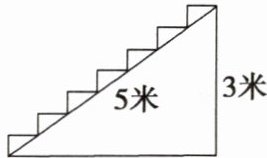
7. 如图所示为某楼梯,测得楼梯的长为$5$米,高$3$米,计划在楼梯表面铺地毯,则地毯的长度至少为______.

答案： 7米

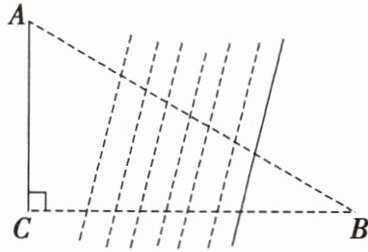
8. 如图,某数学兴趣小组为测量学校$C与河对岸工厂B$之间的距离,在学校附近选一点$A$,利用测量仪器测得$\angle A= 60^{\circ}$,$\angle C= 90^{\circ}$,$AC= 1\mathrm{km}$,据此,可求得学校与工厂之间的距离$BC$等于______$\mathrm{km}$.

答案： $\sqrt{3}$

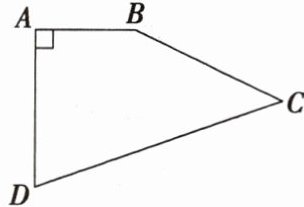
9. 如图,在四边形$ABCD$中,$AB\perp AD$,$AB= 2\mathrm{cm}$,$AD= \sqrt{5}\mathrm{cm}$,$BC= 4\mathrm{cm}$,$CD= 5\mathrm{cm}$,求四边形$ABCD$的面积.

答案：
解:如图，连接BD.
∵∠A=90°,AB=2cm,
　　　　　　　　　　　　　　　　
AD=$\sqrt{5}$cm,
∴BD=$\sqrt{2^{2}+(\sqrt{5})^{2}}$=3(cm).
　又
∵BC=4cm,CD=5cm,
∴CD²=BC²+BD².
∴△BCD是直角三角形，且∠CBD=90°.
∴S四边形ABCD=S△ABD+S△BCD
　=$\frac{1}{2}$AB·AD+$\frac{1}{2}$BC·BD
　=$\frac{1}{2}$×2×$\sqrt{5}$+$\frac{1}{2}$×4×3
　=$\sqrt{5}$+6(cm²).
　故四边形ABCD的面积为($\sqrt{5}$+6)cm².

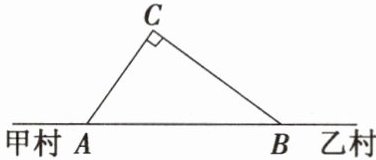
10. 如图,在甲村至乙村的公路旁有一块山地需要开发,现有一$C$处需要爆破,已知点$C与公路上的停靠点A的距离为300$米,与公路上另一停靠点$B的距离为400$米,且$CA\perp CB$,为了安全起见,爆破点$C周围半径300$米范围内不得进入. 请通过计算说明在进行爆破时,公路$AB$段是否有危险需要暂时封锁？若需要封锁,请求出需要封锁的公路长.

答案：
解:公路AB段需要暂时封锁.
　　理由如下:如图，过C作CD⊥AB于点D.
　　　　　　　　
　　由题知,BC=400米,AC=300米,∠ACB=90°,
根据勾股定理，得AB=$\sqrt{AC^{2}+BC^{2}}$=500(米).
∴S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$BC·AC.
∴CD=$\frac{BC·AC}{AB}$=$\frac{400×300}{500}$=240(米).
由于240米＜300米，故有危险,
故公路AB段需要暂时封锁.
如图，设EF为需要封锁的公路，
∵爆破点C周围半径300米范围内不得进入，
∴CE=CF=300米.
∵CD=240米,
∴DE=DF=$\sqrt{CE^{2}-CD^{2}}$=180(米).
∴EF=360米.故需要封锁的公路长为360米.