1. 如图,下列命题中,正确的是 (
①若∠1=∠3,则AD//BC;
②若AD//BC,则∠1=∠2=∠3;
③若∠1=∠3,AD//BC,则∠1=∠2;
④若∠C+∠3+∠4=180°,则AD//BC。
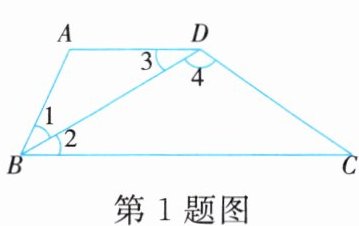
A.①②
B.①③
C.②④
D.③④
D
)①若∠1=∠3,则AD//BC;
②若AD//BC,则∠1=∠2=∠3;
③若∠1=∠3,AD//BC,则∠1=∠2;
④若∠C+∠3+∠4=180°,则AD//BC。

A.①②
B.①③
C.②④
D.③④
答案:
1.D
2. 如图,在下列给出的条件中,不能判定AC//DF的是 (
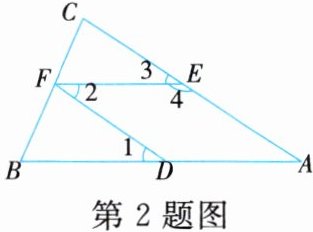
A.∠1=∠2
B.∠4+∠2=180°
C.∠2=∠3
D.∠A=∠1
A
)
A.∠1=∠2
B.∠4+∠2=180°
C.∠2=∠3
D.∠A=∠1
答案:
2.A
3. 如图,点E在BC的延长线上,对于给出的四个条件:①∠1=∠3;②∠2+∠5=180°;③∠4=∠B;④∠D+∠BCD=180°。其中能判断AD//BC的是 (

A.①②
B.①④
C.①③
D.②④
B
)
A.①②
B.①④
C.①③
D.②④
答案:
3.B
4. 将一副三角尺按如图所示的方式摆放在直线m,n之间,∠1=25°,∠2=30°。若想证明m//n,则还需要的条件可以是 (

A.∠3=70°
B.∠4=40°
C.∠5=20°
D.∠4=∠5
A
)
A.∠3=70°
B.∠4=40°
C.∠5=20°
D.∠4=∠5
答案:
4.A
5. 如图,已知∠1=∠3,CD//EF。求证:∠1=∠4。请将过程填写完整。
证明(1)
证明:∵∠1=∠3(已知),
∴∠2=∠3(
∴∠1=
∵CD//EF,
∴
∴∠1=∠4。

证明(1)
证明:∵∠1=∠3(已知),
∴∠2=∠3(
对顶角相等
),∴∠1=
∠2
。∵CD//EF,
∴
∠2
=∠4
(两直线平行,同位角相等
),∴∠1=∠4。

答案:
5.对顶角相等 ∠2 ∠2 ∠4 两直线平行,同位角相等
6. 如图,∠ABD=100°,且BC平分∠ABD,∠1=50°。
(1)求证:AB//CD。
(2)求∠2的度数。
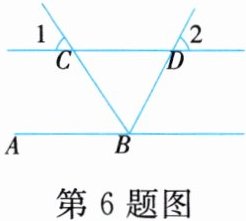
(1)求证:AB//CD。
(2)求∠2的度数。

答案:
1. (1)证明$AB// CD$:
解:因为$BC$平分$\angle ABD$,$\angle ABD = 100^{\circ}$,根据角平分线定义$\angle ABC=\frac{1}{2}\angle ABD$。
所以$\angle ABC=\frac{1}{2}×100^{\circ}=50^{\circ}$。
又因为$\angle1 = 50^{\circ}$,所以$\angle1=\angle ABC$。
根据内错角相等,两直线平行($\angle1$与$\angle ABC$是内错角),可得$AB// CD$。
2. (2)求$\angle2$的度数:
解:因为$AB// CD$,根据两直线平行,同旁内角互补,$\angle ABD+\angle BDC = 180^{\circ}$($\angle ABD$与$\angle BDC$是同旁内角)。
已知$\angle ABD = 100^{\circ}$,则$\angle BDC=180^{\circ}-\angle ABD=180 - 100^{\circ}=80^{\circ}$。
又因为$\angle2$与$\angle BDC$是对顶角,根据对顶角相等$\angle2=\angle BDC$。
所以$\angle2 = 80^{\circ}$。
综上,(1)已证$AB// CD$;(2)$\angle2$的度数为$80^{\circ}$。
解:因为$BC$平分$\angle ABD$,$\angle ABD = 100^{\circ}$,根据角平分线定义$\angle ABC=\frac{1}{2}\angle ABD$。
所以$\angle ABC=\frac{1}{2}×100^{\circ}=50^{\circ}$。
又因为$\angle1 = 50^{\circ}$,所以$\angle1=\angle ABC$。
根据内错角相等,两直线平行($\angle1$与$\angle ABC$是内错角),可得$AB// CD$。
2. (2)求$\angle2$的度数:
解:因为$AB// CD$,根据两直线平行,同旁内角互补,$\angle ABD+\angle BDC = 180^{\circ}$($\angle ABD$与$\angle BDC$是同旁内角)。
已知$\angle ABD = 100^{\circ}$,则$\angle BDC=180^{\circ}-\angle ABD=180 - 100^{\circ}=80^{\circ}$。
又因为$\angle2$与$\angle BDC$是对顶角,根据对顶角相等$\angle2=\angle BDC$。
所以$\angle2 = 80^{\circ}$。
综上,(1)已证$AB// CD$;(2)$\angle2$的度数为$80^{\circ}$。
7. 如图,在△ABC中,点D在边AB上,DE//AC,交BC于点E,点F在边AC上,∠AFD=∠BED。
(1)求证:DF//BC。
(2)若∠A+∠B=120°,求∠FDE的度数。
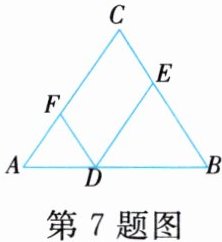
(1)求证:DF//BC。
(2)若∠A+∠B=120°,求∠FDE的度数。

答案:
7.
(1)略
(2)60°
(1)略
(2)60°
查看更多完整答案,请扫码查看


