1. 如图,在△ABC中,AB=AC,∠A=40°,则∠ACD的度数为 (

A.70°
B.100°
C.110°
D.140°
C
)
A.70°
B.100°
C.110°
D.140°
答案:
1.C
2. 如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB= (
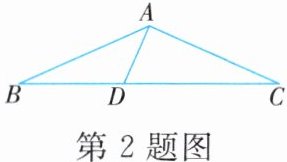
A.100°
B.115°
C.130°
D.145°
B
)
A.100°
B.115°
C.130°
D.145°
答案:
2.B
3. 如图,直线l//m,等边三角形ABC的两个顶点B,C分别落在直线l,m上。若∠ABE=21°,则∠ACD的度数为 (

A.45°
B.39°
C.29°
D.21°
B
)
A.45°
B.39°
C.29°
D.21°
答案:
3.B
4. 若等腰三角形的一个底角的度数为40°,则它的顶角的度数为
100
°。
答案:
4.100
5. 如图,在△ABC中,以点A为圆心,线段AB的长为半径画弧,交BC于点D,连结AD。若∠ABD=55°,则∠ADC=
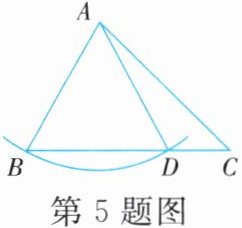
125
°。
答案:
5.125
6. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D。写出图中相等的角

∠A=∠ABD=∠DBC,∠ABC=∠C=∠BDC
。
答案:
6.∠A=∠ABD=∠DBC,∠ABC=∠C=∠BDC
7. 如图,已知线段a和∠1,用直尺和圆规作等腰三角形ABC,使AB=AC=a,∠B=∠1(保留作图痕迹,不写作法)。
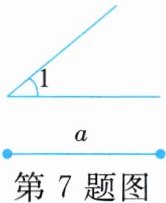

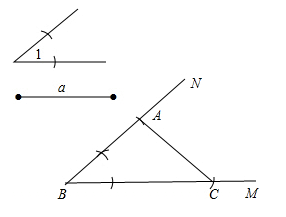
答案:

8. 如图,△ABC是等边三角形,点D,E在直线BC上,DB=EC。求证:∠D=∠E。
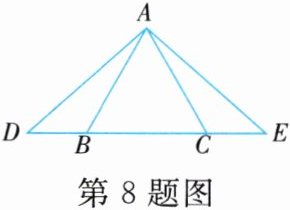

答案:
∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∴∠ABD=180°-∠ABC=120°,∠ACE=180°-∠ACB=120°,
∴∠ABD=∠ACE,
在△ABD和△ACE中,
$\begin{cases}AB=AC \\∠ABD=∠ACE \\DB=EC\end{cases}$
∴△ABD≌△ACE(SAS),
∴∠D=∠E。
∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∴∠ABD=180°-∠ABC=120°,∠ACE=180°-∠ACB=120°,
∴∠ABD=∠ACE,
在△ABD和△ACE中,
$\begin{cases}AB=AC \\∠ABD=∠ACE \\DB=EC\end{cases}$
∴△ABD≌△ACE(SAS),
∴∠D=∠E。
9. 如图,在△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC。若∠BAE=30°,求∠ADC的度数。


答案:
9.75°
查看更多完整答案,请扫码查看


