9. 如图,点$D$在$\triangle ABC$的边$BC$上,点$P$在射线$AD$上(不与点$A$,$D$重合),连结$PB$,$PC$。下列命题中,不一定是真命题的是 (
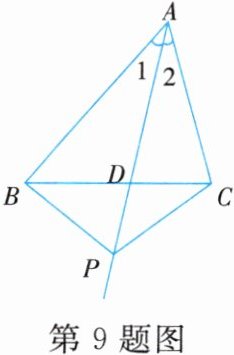
A.若$AB = AC$,$AD\perp BC$,则$PB = PC$
B.若$PB = PC$,$AD\perp BC$,则$AB = AC$
C.若$AB = AC$,$\angle1=\angle2$,则$PB = PC$
D.若$PB = PC$,$\angle1=\angle2$,则$AB = AC$
D
)
A.若$AB = AC$,$AD\perp BC$,则$PB = PC$
B.若$PB = PC$,$AD\perp BC$,则$AB = AC$
C.若$AB = AC$,$\angle1=\angle2$,则$PB = PC$
D.若$PB = PC$,$\angle1=\angle2$,则$AB = AC$
答案:
9.D
10.命题“等腰三角形两腰上的高线长相等”的逆命题是。逆命题是命题(填“真”或“假”)。
答案:
10.两边上的高线长相等的三角形是等腰三角形 真
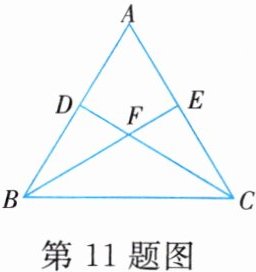
11. 如图,已知在等腰三角形$ABC$中,$AB = AC$,点$D$,$E$分别在边$AB$,$AC$上,且$AD = AE$,连结$BE$,$CD$,两者相交于点$F$。
(1)判断$\angle ABE$与$\angle ACD$之间的数量关系,并说明理由。
(2)求证:过点$A$,$F$的直线垂直平分线段$BC$。
(1)判断$\angle ABE$与$\angle ACD$之间的数量关系,并说明理由。
(2)求证:过点$A$,$F$的直线垂直平分线段$BC$。

答案:
1. (1)
解:$\angle ABE=\angle ACD$。
理由:
在$\triangle ABE$和$\triangle ACD$中,
已知$AB = AC$,$\angle A=\angle A$(公共角),$AE = AD$。
根据全等三角形判定定理中的“边角边”($SAS$),可得$\triangle ABE\cong\triangle ACD$。
再根据全等三角形的性质:全等三角形的对应角相等,所以$\angle ABE=\angle ACD$。
2. (2)
证明:
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
又因为$\angle ABE=\angle ACD$,所以$\angle ABC-\angle ABE=\angle ACB - \angle ACD$,即$\angle FBC=\angle FCB$。
根据等角对等边,可得$FB = FC$。
又因为$AB = AC$,所以点$A$,$F$都在线段$BC$的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上)。
所以过点$A$,$F$的直线垂直平分线段$BC$。
解:$\angle ABE=\angle ACD$。
理由:
在$\triangle ABE$和$\triangle ACD$中,
已知$AB = AC$,$\angle A=\angle A$(公共角),$AE = AD$。
根据全等三角形判定定理中的“边角边”($SAS$),可得$\triangle ABE\cong\triangle ACD$。
再根据全等三角形的性质:全等三角形的对应角相等,所以$\angle ABE=\angle ACD$。
2. (2)
证明:
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
又因为$\angle ABE=\angle ACD$,所以$\angle ABC-\angle ABE=\angle ACB - \angle ACD$,即$\angle FBC=\angle FCB$。
根据等角对等边,可得$FB = FC$。
又因为$AB = AC$,所以点$A$,$F$都在线段$BC$的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上)。
所以过点$A$,$F$的直线垂直平分线段$BC$。
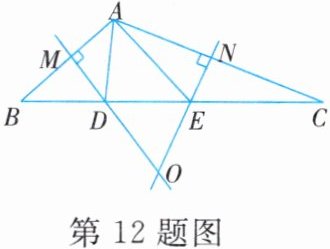
12. 如图,在$\triangle ABC$中,边$AB$,$AC$的垂直平分线分别交$BC$于点$D$,$E$,直线$DM$,$EN$相交于点$O$。
(1)试判断点$O$是否在$BC$的垂直平分线上,并说明理由。
(2)若$\angle BAC = 100^{\circ}$,求$\angle MON$的度数。
(1)试判断点$O$是否在$BC$的垂直平分线上,并说明理由。
(2)若$\angle BAC = 100^{\circ}$,求$\angle MON$的度数。

答案:
12.
(1)点 O 在 BC 的垂直平分线上。理由略
(2)80°
(1)点 O 在 BC 的垂直平分线上。理由略
(2)80°
13. [推理能力](1)已知命题:“$P$为等边三角形$ABC$内一点,若点$P$到三边的距离相等,则$PA=PB = PC$。”写出它的逆命题,判断其逆命题是否成立。若成立,请给出证明。
(2)进一步证明:等边三角形$ABC$内一点$P$到各边的距离之和为定值。
(2)进一步证明:等边三角形$ABC$内一点$P$到各边的距离之和为定值。
答案:
13.
(1)逆命题:P 为等边三角形 ABC 内一点,若 PA=PB=PC,则点 P 到三边的距离相等。该逆命题成立。证明略
(2)略
(1)逆命题:P 为等边三角形 ABC 内一点,若 PA=PB=PC,则点 P 到三边的距离相等。该逆命题成立。证明略
(2)略
查看更多完整答案,请扫码查看


