《2025年智趣夏令营四年级玩转数学冀教版》

1. 根据加法运算律填空。
(1)$x+y= ( )+( )$
(2)$a+(b+c)= (+)+( )$

答案： 解析：
题目考查的是加法交换律和加法结合律。
对于第一个表达式，根据加法交换律，两个数相加，交换加数的位置和不变，即$x+y=y+x$。
对于第二个表达式，根据加法结合律，三个数相加，先把前两个数相加，或者先把后两个数相加，和不变，即$a+(b+c)=(a+b)+c$。
答案：
(1)$x+y= (y)+(x)$，
(2)$a+(b+c)= (a+b)+(c)$。

2. 如果用 x 表示长方形的长,用 y 表示长方形的宽,那么长方形的周长$C= $ ( ),面积$S= ( )$。

答案： 解析：
本题考查长方形的周长和面积公式。
长方形的周长是两倍的长加上两倍的宽，即$C = 2x + 2y$。
长方形的面积是长乘以宽，即$S = xy$。
答案：
$C = 2(x + y)$；$S = xy$。

3. 张老师每小时能折 a 只纸鹤,红红每小时比张老师少折 b 只。
(1)$a-b$表示____;
(2)4a 表示____;
(3)$4(a-b)$表示____。

答案： 解析：
(1) $a-b$ 表示红红每小时折纸鹤的个数。因为张老师每小时能折a只纸鹤，红红每小时比张老师少折b只，所以红红每小时折的纸鹤数为 $a-b$。
(2) $4a$ 表示张老师4小时折纸鹤的总数。因为张老师每小时能折a只纸鹤，所以4小时就能折 $4 × a = 4a$ 只纸鹤。
(3) $4(a-b)$ 表示红红4小时折纸鹤的总数。因为红红每小时折 $a-b$ 只纸鹤，所以4小时就能折 $4 × (a-b) = 4(a-b)$ 只纸鹤。
答案：
(1) $a-b$ 表示红红每小时折纸鹤的个数。
(2) $4a$ 表示张老师4小时折纸鹤的总数。
(3) $4(a-b)$ 表示红红4小时折纸鹤的总数。

4. 按要求完成下面各题。
(1)用字母表示出图形①的周长。

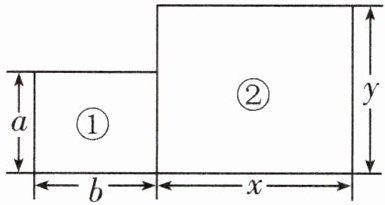
(2)用字母表示出图形②的周长。
(3)图形①的面积与图形②的面积和是多少?

答案： 解析：本题主要考查长方形周长和面积的计算以及对用字母表示数的理解。
(1)图形①是一个长为$b$，宽为$a$的长方形，根据长方形周长公式$C=(长 + 宽)×2$，可得其周长为$2(a + b)$。
(2)图形②是一个长为$x$，宽为$y$的长方形，同样根据长方形周长公式，可得其周长为$2(x + y)$。
(3)图形①的面积根据长方形面积公式$S = 长×宽$，可得$S_1 = ab$；图形②的面积为$S_2 = xy$。那么它们的面积和就是$ab + xy$。
答案：
(1)$2(a + b)$；
(2)$2(x + y)$；
(3)$ab + xy$。