《2025年智趣夏令营四年级玩转数学冀教版》

1. 按角分,下面的三角形各是什么三角形?

( ) ( ) ( )

答案： 解析：本题考查三角形的分类。
第一个三角形有一个角是锐角，但无法看出其他两个角的大小，但通过量角器测量可知其他两个角也是锐角，三个角都是锐角的三角形是锐角三角形；
第二个三角形有一个角是直角，是直角三角形；
第三个三角形有一个角是钝角，是钝角三角形。
答案：锐角三角形，直角三角形，钝角三角形。

2. 我是小法官。(对的打“√”,错的打“×”)
(1) 平行四边形是只有一组对边平行的四边形。 ( )
(2) 平行四边形只能画一条高。 ( )
(3) 在同一平面内,两条直线永不相交,就一定平行。 ( )
(4) 两条直线相交成直角时,这两条直线互相垂直。 ( )

答案： 解析：本题考查的是平行四边形和直线的性质以及对平行和垂直概念的理解。
(1) 平行四边形的定义是两组对边分别平行，而题目中说只有一组对边平行，这与平行四边形的定义不符，实际是梯形的定义。所以判断为错。
(2) 平行四边形可以从一边上任意一点向对边作高，因此可以作无数条高。所以题目中说只能画一条高是错误的。
(3) 根据平行的定义，同一平面内不相交的两条直线称为平行线。所以题目的说法是正确的。
(4) 当两条直线相交并且形成直角时，这两条直线就是互相垂直的。所以题目的说法是正确的。
答案：
(1)×
(2)×
(3)√
(4)√。

3. 我会选择。
(1) 有一个角是直角的平行四边形一定是( )。
①长方形 ②正方形 ③梯形
(2) 下面三句话中,错误的是( )。
①长方形是特殊的平行四边形
②平行四边形也是四边形
③平行四边形具有稳定性

答案： 解析：
(1) 本题考查的是平行四边形的性质以及长方形和正方形的定义。有一个角是直角的平行四边形，由于平行四边形的对角相等，相邻两角互补，所以它一定是长方形。正方形还需要所有边等长，而梯形则不是平行四边形。
(2) 本题考查的是对平行四边形性质的理解。长方形是特殊的平行四边形，因为长方形的对边平行且等长，且四个角都是直角，满足平行四边形的定义。平行四边形是四边形的一种，因为它有四条边。但是，平行四边形并不具有稳定性，稳定性是三角形特有的性质，因为三角形具有确定性，而平行四边形则可以在保持对边平行的情况下进行变形。
答案：
(1) ①长方形
(2) ③平行四边形具有稳定性

4. 指出下列三角形中未知角的度数。
(1)

答案： 解析：本题考查三角形内角和定理的应用，即三角形的内角和为$180^{\circ}$。
答案：（1）$180^{\circ}-50^{\circ}-47^{\circ}=83^{\circ}$，所以未知角的度数为$83^{\circ}$。
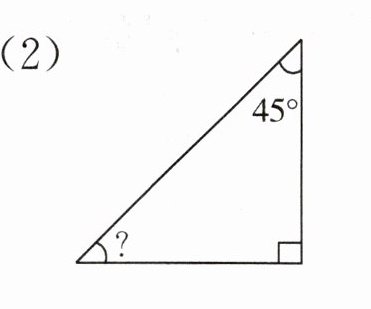
（2）$180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$，所以未知角的度数为$45^{\circ}$。