《2025年暑假Happy假日八年级物理通用版》

21. 如图,用细线系住一个小球并挂在墙壁上静止,请画出小球对墙壁的压力F的示意图。

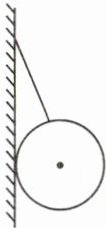
答案：

22. 如图所示是“探究压力作用效果与哪些因素有关”的实验。

(1)实验中是通过观察海绵的____来比较压力的作用效果。
(2)通过比较甲、乙两图中的实验现象,可以得出结论:在____一定时,压力越大,压力的作用效果越明显;通过比较图乙和图____可说明,压力一定时,受力面积越小,压力的作用效果越明显。
(3)如果实验中利用如图丁所示的木板代替海绵,____(选填“可以”或“不可以”)完成该实验,理由是____不明显,不能反映压力的作用效果。

答案： 【解析】：
(1) 实验中是通过观察海绵的**凹陷程度**来比较压力的作用效果，这是转换法的应用。
(2) 甲、乙两图，受力面积相同，压力不同，通过比较甲、乙两图中的实验现象，可以得出结论：在**受力面积**一定时，压力越大，压力的作用效果越明显；探究压力的作用效果与受力面积的关系时，应控制压力的大小不变，通过比较图乙和图**丙**可说明，压力一定时，受力面积越小，压力的作用效果越明显。
(3) 如果实验中利用如图丁所示的木板代替海绵，**不可以**完成该实验，理由是**木板形变**不明显，不能反映压力的作用效果。
【答案】：
(1) 凹陷程度
(2) 受力面积；丙
(3) 不可以；木板形变

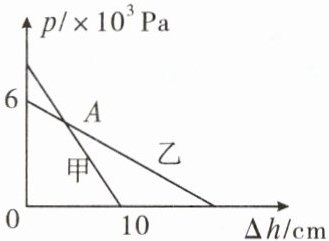
23.【科学思维】质量分布均匀的实心正方体甲、乙放在水平地面上,将甲、乙沿水平方向切去高度$\Delta h$,剩余部分对地面的压强$p$与切去高度$\Delta h$的关系如图所示,已知甲的密度$\rho_{甲}=8×10^{3}kg/m^{3}$,乙的边长为20cm。($g$取$10N/kg$)求:
(1)甲的质量。
(2)乙的密度。
(3)在A点时,甲对地面的压强。

答案： 【解析】：
### （1）求甲的质量
- 由图可知，当$\Delta h_{甲}=10cm = 0.1m$时，甲对地面压强$p_{甲}=0$，这表明甲的边长$h_{甲}=0.1m$。
- 根据密度公式$\rho=\frac{m}{V}$，甲的体积$V_{甲}=h_{甲}^{3}=(0.1m)^{3}=1\times10^{-3}m^{3}$。
- 已知$\rho_{甲}=8\times10^{3}kg/m^{3}$，则甲的质量$m_{甲}=\rho_{甲}V_{甲}=8\times10^{3}kg/m^{3}\times1\times10^{-3}m^{3}=8kg$。
### （2）求乙的密度
对于质量分布均匀的实心正方体，对地面压强$p = \rho gh$。
由图知，当$\Delta h = 0$时，乙对地面压强$p_{乙}=6\times10^{3}Pa$，乙的边长$h_{乙}=20cm = 0.2m$。
根据$p = \rho gh$，可得乙的密度$\rho_{乙}=\frac{p_{乙}}{gh_{乙}}=\frac{6\times10^{3}Pa}{10N/kg\times0.2m}=3\times10^{3}kg/m^{3}$。
### （3）求在$A$点时甲对地面的压强
设切去高度为$\Delta h$，甲剩余部分对地面压强$p_{甲剩}=\rho_{甲}g(h_{甲}-\Delta h)$，乙剩余部分对地面压强$p_{乙剩}=\rho_{乙}g(h_{乙}-\Delta h)$。
在$A$点$p_{甲剩}=p_{乙剩}$，即$\rho_{甲}g(h_{甲}-\Delta h)=\rho_{乙}g(h_{乙}-\Delta h)$。
把$\rho_{甲}=8\times10^{3}kg/m^{3}$，$h_{甲}=0.1m$，$\rho_{乙}=3\times10^{3}kg/m^{3}$，$h_{乙}=0.2m$代入可得：
$8\times10^{3}kg/m^{3}\times(0.1m - \Delta h)=3\times10^{3}kg/m^{3}\times(0.2m - \Delta h)$
$8\times(0.1 - \Delta h)=3\times(0.2 - \Delta h)$
$0.8 - 8\Delta h = 0.6 - 3\Delta h$
$5\Delta h = 0.2$
$\Delta h = 0.04m$。
则在$A$点时甲对地面压强$p_{甲A}=\rho_{甲}g(h_{甲}-\Delta h)=8\times10^{3}kg/m^{3}\times10N/kg\times(0.1m - 0.04m)=4.8\times10^{3}Pa$。
【答案】：
(1) 甲的质量为$\boldsymbol{8kg}$。
(2) 乙的密度为$\boldsymbol{3\times10^{3}kg/m^{3}}$。
(3) 在$A$点时，甲对地面的压强为$\boldsymbol{4.8\times10^{3}Pa}$。