《2025年暑假作业五年级数学人教版黄山书社》

1. 右图是一个机器零件。现在要对这个零件进行表面电镀防锈处理。需要电镀的面积有多大？

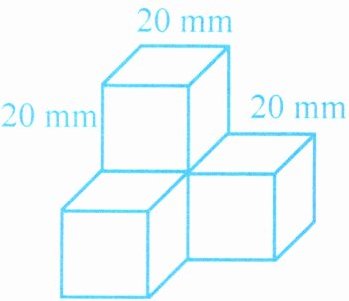
答案： 【解析】：
1. 首先分析正方体一个面的面积：
已知正方体棱长$a = 20mm$，根据正方形面积公式$S=a^{2}$，可得一个面的面积$S = 20×20=400mm^{2}$。
2. 然后数这个组合体表面的面的数量：
从上下、前后、左右观察这个组合体。
上面和下面：通过观察，上面和下面看到的面的数量都是$3$个；前面和后面看到的面的数量都是$3$个；左面和右面看到的面的数量都是$3$个。
那么这个组合体表面的面的总数$n=(3 + 3+3)×2=18$个。
3. 最后计算电镀面积：
因为电镀面积就是这个组合体的表面积，而表面积等于一个面的面积乘以面的总数。
所以电镀面积$A = 400×18 = 7200mm^{2}$。
【答案】：$7200mm^{2}$

2. 一间教室长9m,宽6m,高3.5m,现要给教室的顶部和四壁粉刷乳胶漆,除去门窗$25m^2,$这间教室的粉刷面积一共是多少平方米？

答案： 【解析】：本题可先分别求出教室顶部和四壁的面积，再将它们相加得到总面积，最后减去门窗的面积，即可得到需要粉刷的面积。
**步骤一：计算教室顶部的面积**
教室顶部是一个长$9m$、宽$6m$的长方形，根据长方形面积公式$S = a× b$（其中$S$为长方形面积，$a$为长方形的长，$b$为长方形的宽），可得教室顶部的面积为：$9×6 = 54$（平方米）
**步骤二：计算教室四壁的面积**
教室的四壁包括两个长为$9m$、宽为$3.5m$的面和两个长为$6m$、宽为$3.5m$的面。
计算长为$9m$、宽为$3.5m$的面的面积：根据长方形面积公式可得，一个这样的面的面积为$9×3.5 = 31.5$平方米，那么两个这样的面的面积为$2×31.5 = 63$平方米。
计算长为$6m$、宽为$3.5m$的面的面积：同理可得，一个这样的面的面积为$6×3.5 = 21$平方米，那么两个这样的面的面积为$2×21 = 42$平方米。
所以教室四壁的总面积为$63 + 42 = 105$平方米。
**步骤三：计算需要粉刷的总面积**
将教室顶部的面积和四壁的面积相加，可得总面积为$54 + 105 = 159$平方米。
因为要除去门窗面积$25$平方米，所以这间教室的粉刷面积为$159 - 25 = 134$平方米。
【答案】：$134$

3. 永康小学挖一个沙坑,量得沙坑长5m,宽2.5m,深60cm,这个沙坑最多能装沙多少立方米？

答案： 【解析】：本题可根据长方体的体积公式来计算沙坑的容积，也就是能装沙的体积。首先需要统一单位，将沙坑深度$60cm$换算为$0.6m$，然后根据长方体体积公式$V = a× b× h$（其中$V$表示体积，$a$表示长，$b$表示宽，$h$表示高），把长$5m$、宽$2.5m$、深$0.6m$代入公式进行计算。
【答案】：$7.5$

4. 一个无盖的长方体木箱,长8分米,宽6分米,高4分米。如果油漆这个木箱,油漆的面积是多少平方米？

答案： 【解析】：本题可根据长方体表面积公式来计算油漆的面积。由于该木箱无盖，所以只需要求出这个长方体$5$个面的面积之和即可。
长方体$5$个面的面积和$=$长$×$宽$+$长$×$高$×2 +$宽$×$高$×2$。
已知长方体木箱长$8$分米、宽$6$分米、高$4$分米，将数值代入公式可得：
$8×6 + 8×4×2 + 6×4×2$
$= 48 + 64 + 48$
$= 160$（平方分米）
因为$1$平方米$ = 100$平方分米，所以$160$平方分米换算成平方米为：$160÷100 = 1.6$平方米。
【答案】：$1.6$平方米

5. 一段长2米的长方体木料,将它截成5段后,表面积增加了40平方分米,这根木料的体积是多少立方分米？

答案： 【解析】：把这个长方体木料截成5段，需要截4次，每截一次增加两个底面面积，所以一共增加了$2×4 = 8$个底面面积。已知表面积增加了40平方分米，那么一个底面面积为$40÷8 = 5$平方分米。长方体体积公式为$V=Sh$（$S$是底面积，$h$是高），题目中木料长2米，换算单位后$2$米$ = 20$分米，所以木料体积为$5×20 = 100$立方分米。
【答案】：100