《2025年文轩图书假期生活指导暑八年级物理》

16. 小金把家里景观水池底部的鹅卵石取出清洗。他先将一个重为$10N$的空桶漂浮在水面上,然后将池底的鹅卵石捞出放置在桶内,桶仍漂浮在水面。(不考虑捞出过程中带出的水,$\rho_{水}= 1.0×10^{3}kg/m^{3}$)

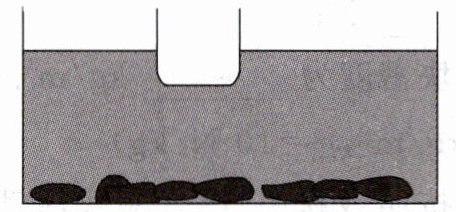
(1)空桶漂浮在水面时所受浮力大小；
(2)鹅卵石捞出放置在桶内时,水池水面高度与鹅卵石未捞出时相比会______(填“上升”“下降”或“不变”)。若此时桶排开水的体积为$6.0×10^{-3}m^{3}$,求桶内鹅卵石的质量。

答案： 解:
(1) 空桶漂浮在水面上, 所以浮力等于重力, 即 $ F_{浮} = G_{桶} = 10N $;
(2) 鹅卵石捞出前沉底, 浮力小于重力, 即 $ F_{浮1} ＜ G $, 将鹅卵石捞出放置在桶内时, 鹅卵石与小桶都处于漂浮状态, 此时鹅卵石的浮力等于重力, 即 $ F_{浮2} = G $, 所以 $ F_{浮1} ＜ F_{浮2} $, 即鹅卵石捞出放置在桶内时鹅卵石的浮力变大, 根据 $ F_{浮} = \rho_{液}gV_{排} $ 知排开水的体积变大, 水池水面高度与鹅卵石未捞出时相比会上升;
鹅卵石捞出放置在桶内时的浮力为:
$ F_{浮}' = \rho_{水}gV_{排}' = 1.0 × 10^{3}kg/m^{3} × 10N/kg × 6.0 × 10^{-3}m^{3} = 60N $,
桶内鹅卵石的重力为:
$ G_{石} = F_{浮}' - G_{桶} = 60N - 10N = 50N $,
鹅卵石的质量为: $ m_{石} = \frac{G_{石}}{g} = \frac{50N}{10N/kg} = 5kg $.

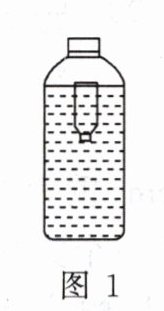
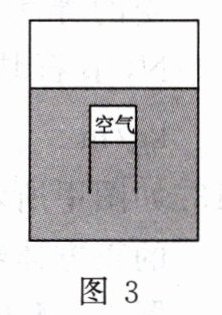
17. “浮沉子”最早是由科学家笛卡儿设计的。小华用大塑料瓶(大瓶)和开口小玻璃瓶(小瓶)制作了图1所示的“浮沉子”；装有适量水的小瓶开口朝下漂浮在大瓶内的水面上,拧紧大瓶的瓶盖使其密封,两瓶内均有少量空气。将小瓶视为圆柱形容器,底面积为$S$,忽略其壁厚(即忽略小瓶自身的体积)。当小瓶漂浮时,简化的模型如图2所示,小瓶内空气柱的高度为$h$,手握大瓶施加适当的压力,使小瓶下沉并恰好悬浮在图3所示的位置。将倒置的小瓶和小瓶内的空气看成一个整体A,A的质量为$m$,水的密度为$\rho_{水}$,为已知量,求：



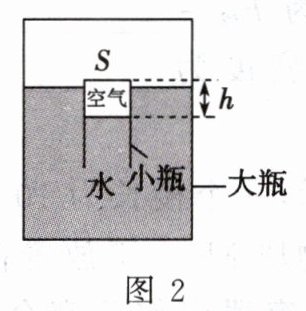
(1)图2中A所受浮力的大小；
(2)图2中A排开水的体积；
(3)图2和图3中小瓶内空气的密度之比。

答案： 解:
(1) 由图 2 可知, A 处于漂浮状态,
由物体的漂浮条件可知, 图 2 中 A 所受浮力:
$ F_{浮} = G = mg $;
(2) 由 $ F_{浮} = \rho_{液}gV_{排} $ 可知, 图 2 中 A 排开水的体积:
$ V_{排} = \frac{F_{浮}}{\rho_{水}g} = \frac{mg}{\rho_{水}g} = \frac{m}{\rho_{水}} $;
(3) 图 2 中小瓶内空气的体积为 $ V = Sh $,
由图 3 可知, A 处于悬浮状态,
由物体的悬浮条件可知, 图 3 中 A 所受浮力:
$ F_{浮}' = G = mg $,
由 $ F_{浮} = \rho_{液}gV_{排} $ 可知, 图 3 中 A 排开水的体积:
$ V_{排}' = \frac{F_{浮}'}{\rho_{水}g} = \frac{mg}{\rho_{水}g} = \frac{m}{\rho_{水}} $,
因为忽略小瓶自身的体积, 所以图 3 中空气的体积:
$ V' = V_{排}' = \frac{m}{\rho_{水}} $,
由于图 2 和图 3 中小瓶内空气的质量不变,
由 $ \rho = \frac{m}{V} $ 可知, 图 2 和图 3 中小瓶内空气的密度之比:
$ \frac{\rho_{空}}{\rho_{空}'} = \frac{\frac{mg}{V}}{\frac{m}{V'}} = \frac{V'}{V} = \frac{\frac{m}{\rho_{水}}}{Sh} = \frac{m}{Sh\rho_{水}} $.