2025年暑假作业新疆青少年出版社八年级物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业新疆青少年出版社八年级物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图所示的平底容器,其质量为 $ 0.2 \, \text{kg} $,底面积为 $ 3 × 10^{-3} \, \text{m}^2 $,内装有 $ 1 \, \text{kg} $ 的水,测得容器中水的深度为 $ 20 \, \text{cm} $,若将该容器放在面积为 $ 1.5 \, \text{m}^2 $ 的水平桌面中央, $ g $ 取 $ 10 \, \text{N/kg} $,则:
(1) 容器对桌面的压强为多少?
(2) 水对容器底部的压强为多少?
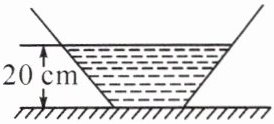
(1) 容器对桌面的压强为多少?
(2) 水对容器底部的压强为多少?

答案:
(1) 容器对桌面的压力 $ F = G = (m_{容} + m_{水})g = (0.2\ \text{kg} + 1\ \text{kg}) \times 10\ \text{N/kg} = 12\ \text{N} $,容器对桌面的压强 $ p = \frac{F}{S} = \frac{12\ \text{N}}{3 \times 10^{-3}\ \text{m}^2} = 4 \times 10^3\ \text{Pa} $
(2) 水对容器底部的压强 $ p' = \rho gh = 1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg} \times 20 \times 10^{-2}\ \text{m} = 2 \times 10^3\ \text{Pa} $
(1) 容器对桌面的压力 $ F = G = (m_{容} + m_{水})g = (0.2\ \text{kg} + 1\ \text{kg}) \times 10\ \text{N/kg} = 12\ \text{N} $,容器对桌面的压强 $ p = \frac{F}{S} = \frac{12\ \text{N}}{3 \times 10^{-3}\ \text{m}^2} = 4 \times 10^3\ \text{Pa} $
(2) 水对容器底部的压强 $ p' = \rho gh = 1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg} \times 20 \times 10^{-2}\ \text{m} = 2 \times 10^3\ \text{Pa} $
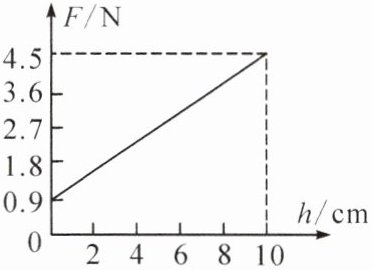
2. 将平底薄壁直圆筒状的空杯放在饮料机的水平杯座上接饮料,杯座受到的压力 $ F $ 随杯中饮料的高度 $ h $ 变化的图像如图所示。饮料出口的横截面积 $ S_1 = 0.8 \, \text{cm}^2 $,饮料流出的速度 $ v = 50 \, \text{cm/s} $,杯高 $ H = 10 \, \text{cm} $,杯底面积 $ S_2 = 30 \, \text{cm}^2 $, $ g $ 取 $ 10 \, \text{N/kg} $。求:
(1) 装满饮料时,杯底受到饮料的压力为多大?
(2) 饮料的密度为多大?
(3) 设杯底与杯座的接触面积也为 $ S_2 $,饮料持续流入空杯 $ 5 \, \text{s} $ 后关闭开关,杯对杯座的压强为多大?
(1) 装满饮料时,杯底受到饮料的压力为多大?
(2) 饮料的密度为多大?
(3) 设杯底与杯座的接触面积也为 $ S_2 $,饮料持续流入空杯 $ 5 \, \text{s} $ 后关闭开关,杯对杯座的压强为多大?

答案:
(1) 由图可知空杯对杯座的压力 $ F_0 = 0.9\ \text{N} $,装满饮料时,杯对杯座的压力 $ F_1 = 4.5\ \text{N} $,因杯子为平底薄壁直圆筒状,所以杯底受到饮料的压力 $ F = F_1 - F_0 = 4.5\ \text{N} - 0.9\ \text{N} = 3.6\ \text{N} $
(2) 饮料的质量 $ m = \frac{G}{g} = \frac{F}{g} = \frac{3.6\ \text{N}}{10\ \text{N/kg}} = 0.36\ \text{kg} $,杯中饮料的体积 $ V = S_2H = 30\ \text{cm}^2 \times 10\ \text{cm} = 300\ \text{cm}^3 = 3 \times 10^{-4}\ \text{m}^3 $,则饮料的密度 $ \rho = \frac{m}{V} = \frac{0.36\ \text{kg}}{3 \times 10^{-4}\ \text{m}^3} = 1.2 \times 10^3\ \text{kg/m}^3 $
(3) 饮料持续流入空杯 $ 5\ \text{s} $,则流入杯中饮料的质量 $ m_1 = \rho S_1 vt = 1.2 \times 10^3\ \text{kg/m}^3 \times 0.8 \times 10^{-4}\ \text{m}^2 \times 0.5\ \text{m/s} \times 5\ \text{s} = 0.24\ \text{kg} $,此时饮料对杯底的压力 $ F_2 = m_1g = 0.24\ \text{kg} \times 10\ \text{N/kg} = 2.4\ \text{N} $,此时杯对杯座的压强 $ p = \frac{F_0 + F_2}{S_2} = \frac{0.9\ \text{N} + 2.4\ \text{N}}{30 \times 10^{-4}\ \text{m}^2} = 1.1 \times 10^3\ \text{Pa} $
(1) 由图可知空杯对杯座的压力 $ F_0 = 0.9\ \text{N} $,装满饮料时,杯对杯座的压力 $ F_1 = 4.5\ \text{N} $,因杯子为平底薄壁直圆筒状,所以杯底受到饮料的压力 $ F = F_1 - F_0 = 4.5\ \text{N} - 0.9\ \text{N} = 3.6\ \text{N} $
(2) 饮料的质量 $ m = \frac{G}{g} = \frac{F}{g} = \frac{3.6\ \text{N}}{10\ \text{N/kg}} = 0.36\ \text{kg} $,杯中饮料的体积 $ V = S_2H = 30\ \text{cm}^2 \times 10\ \text{cm} = 300\ \text{cm}^3 = 3 \times 10^{-4}\ \text{m}^3 $,则饮料的密度 $ \rho = \frac{m}{V} = \frac{0.36\ \text{kg}}{3 \times 10^{-4}\ \text{m}^3} = 1.2 \times 10^3\ \text{kg/m}^3 $
(3) 饮料持续流入空杯 $ 5\ \text{s} $,则流入杯中饮料的质量 $ m_1 = \rho S_1 vt = 1.2 \times 10^3\ \text{kg/m}^3 \times 0.8 \times 10^{-4}\ \text{m}^2 \times 0.5\ \text{m/s} \times 5\ \text{s} = 0.24\ \text{kg} $,此时饮料对杯底的压力 $ F_2 = m_1g = 0.24\ \text{kg} \times 10\ \text{N/kg} = 2.4\ \text{N} $,此时杯对杯座的压强 $ p = \frac{F_0 + F_2}{S_2} = \frac{0.9\ \text{N} + 2.4\ \text{N}}{30 \times 10^{-4}\ \text{m}^2} = 1.1 \times 10^3\ \text{Pa} $
3. 如图所示,一容器放在水平桌上,容器内装有 $ 0.2 \, \text{m} $ 深的水。 $ (\rho_{\text{水}} = 1.0 × 10^3 \, \text{kg/m}^3 $, $ g $ 取 $ 10 \, \text{N/kg}) $ 求:
(1) 水对容器底的压强。
(2) 如果将体积为 $ 200 \, \text{cm}^3 $,密度为 $ 0.8 × 10^3 \, \text{kg/m}^3 $ 的木块放入水中,待木块静止后,浸在水中的体积有多大?
(3) 取出木块,再将体积为 $ 100 \, \text{cm}^3 $,重 $ 1.8 \, \text{N} $ 的一块固体放入水中,当固体浸没在水中静止时,容器底部对它的支持力有多大?

(1) 水对容器底的压强。
(2) 如果将体积为 $ 200 \, \text{cm}^3 $,密度为 $ 0.8 × 10^3 \, \text{kg/m}^3 $ 的木块放入水中,待木块静止后,浸在水中的体积有多大?
(3) 取出木块,再将体积为 $ 100 \, \text{cm}^3 $,重 $ 1.8 \, \text{N} $ 的一块固体放入水中,当固体浸没在水中静止时,容器底部对它的支持力有多大?

答案:
(1) 容器底部受到的水的压强 $ p = \rho_{水}gh = 1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg} \times 0.2\ \text{m} = 2000\ \text{Pa} $
(2) 木块的质量 $ m_{木} = \rho_{木}V_{木} = 0.8 \times 10^3\ \text{kg/m}^3 \times 200 \times 10^{-6}\ \text{m}^3 = 0.16\ \text{kg} $,木块所受重力 $ G_{木} = m_{木}g = 0.16\ \text{kg} \times 10\ \text{N/kg} = 1.6\ \text{N} $,由于 $ \rho_{木} < \rho_{水} $,所以,木块在水中静止后处于漂浮状态,则 $ F_{浮} = G_{木} = 1.6\ \text{N} $,由 $ F_{浮} = \rho_{液}gV_{排} $ 可得木块排开水的体积(即浸在水中的体积) $ V_{排} = \frac{F_{浮}}{\rho_{水}g} = \frac{1.6\ \text{N}}{1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg}} = 1.6 \times 10^{-4}\ \text{m}^3 $
(3) 当固体浸没在水中时,排开水的体积 $ V_{排}' = V_{固体} = 100\ \text{cm}^3 = 1 \times 10^{-4}\ \text{m}^3 $,则固体受到的浮力 $ F_{浮}' = \rho_{水}gV_{排}' = 1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg} \times 1 \times 10^{-4}\ \text{m}^3 = 1\ \text{N} < 1.8\ \text{N} $,即 $ F_{浮}' < G_{固体} $,所以固体在水中静止时沉在容器底部,容器底部对它的支持力 $ F_{支} = G_{固体} - F_{浮}' = 1.8\ \text{N} - 1\ \text{N} = 0.8\ \text{N} $
(1) 容器底部受到的水的压强 $ p = \rho_{水}gh = 1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg} \times 0.2\ \text{m} = 2000\ \text{Pa} $
(2) 木块的质量 $ m_{木} = \rho_{木}V_{木} = 0.8 \times 10^3\ \text{kg/m}^3 \times 200 \times 10^{-6}\ \text{m}^3 = 0.16\ \text{kg} $,木块所受重力 $ G_{木} = m_{木}g = 0.16\ \text{kg} \times 10\ \text{N/kg} = 1.6\ \text{N} $,由于 $ \rho_{木} < \rho_{水} $,所以,木块在水中静止后处于漂浮状态,则 $ F_{浮} = G_{木} = 1.6\ \text{N} $,由 $ F_{浮} = \rho_{液}gV_{排} $ 可得木块排开水的体积(即浸在水中的体积) $ V_{排} = \frac{F_{浮}}{\rho_{水}g} = \frac{1.6\ \text{N}}{1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg}} = 1.6 \times 10^{-4}\ \text{m}^3 $
(3) 当固体浸没在水中时,排开水的体积 $ V_{排}' = V_{固体} = 100\ \text{cm}^3 = 1 \times 10^{-4}\ \text{m}^3 $,则固体受到的浮力 $ F_{浮}' = \rho_{水}gV_{排}' = 1.0 \times 10^3\ \text{kg/m}^3 \times 10\ \text{N/kg} \times 1 \times 10^{-4}\ \text{m}^3 = 1\ \text{N} < 1.8\ \text{N} $,即 $ F_{浮}' < G_{固体} $,所以固体在水中静止时沉在容器底部,容器底部对它的支持力 $ F_{支} = G_{固体} - F_{浮}' = 1.8\ \text{N} - 1\ \text{N} = 0.8\ \text{N} $
查看更多完整答案,请扫码查看


