《2025年亮点给力提优课时作业本九年级物理上册苏科版》

27. 亮点原创 (8分)小亮居住的小区地下车库层高4m,他要将一桶12L的饮用水从车库搬至地面层,有两种方法：一是从车库走楼梯直接搬至地面层；二是把桶装水放在质量为5kg的平板推车(如图)上,从车库出口沿长20m的坡道匀速推至地面层。(桶的质量不计,$\rho_{水}= 1.0×10^{3}kg/m^{3}$,$g$取10N/kg)则：
(1)从车库走楼梯直接搬时,克服桶装水的重力做的功为多少？
(2)用平板推车推至地面层过程中,小亮的推力$F= 90N$,且平行于坡道,则该过程中小亮做的额外功为多少？坡道的机械效率约为多少？

答案： （1）480J　（2）1320J　26.7%　解析:（1）桶的质量不计，则桶装水的质量$m = ρ_{水}V = 1.0×10^3kg/m^3×12×10^{-3}m^3 = 12kg$，桶装水的重力$G = mg = 12kg×10N/kg = 120N$，则从车库走楼梯直接搬到地面层，克服桶装水的重力做的功$W_G = Gh = 120N×4m = 480J$。（2）用平板推车推至地面时，小亮的推力F做的有用功$W_{有用} = W_G = 480J$，推力做的总功$W_{总} = Fs = 90N×20m = 1800J$，则小亮做的额外功$W_{额外} = W_{总} - W_{有用} = 1800J - 480J = 1320J$，所以坡道的机械效率$η = \frac{W_{有用}}{W_{总}}×100\% = \frac{480J}{1800J}×100\% ≈ 26.7\%$。

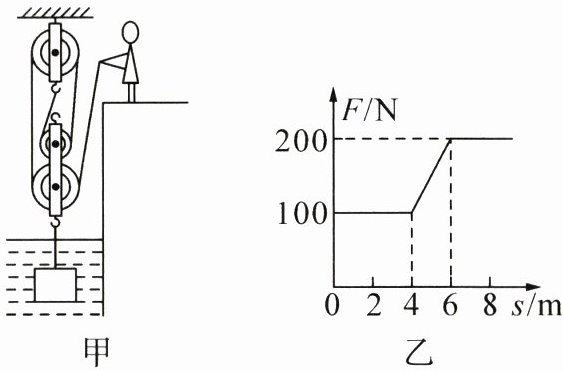
28. (12分)小梦通过如图甲所示的滑轮组将水中物体匀速提升至空中,所用拉力$F与绳端移动的距离s$的关系图像如图乙所示。其中物体在空中匀速上升过程中滑轮组的机械效率为85%,每个滑轮等重,不计绳重、摩擦和水的阻力。则：
(1)物体在空中上升1m,小梦做的功是多少？
(2)物体浸没在水中时所受的浮力是多少？
(3)物体在水中匀速上升过程中滑轮组的机械效率是多少？

答案： （1）800J　（2）400N　（3）70%　解析:由图乙可知，s为0～4m时，拉力为100N，此时物体浸没在水中，s为4～6m时，物体逐渐露出水面，拉力不断增大，s超过6m后，物体完全露出水面，拉力为200N。（1）由图甲可知，动滑轮上绳子的段数$n = 4$，所以物体在空中上升1m，绳子自由端移动的距离$s = nh = 4×1m = 4m$，小梦做的功$W_{总} = Fs = 200N×4m = 800J$。（2）由题意知，物体在空中匀速上升过程中滑轮组的机械效率为85%，则物体在空中上升1m时，拉力做的有用功$W_{有用} = ηW_{总} = 85\%×800J = 680J$，由$W = Gh$可得，物体的重力$G = \frac{W_{有用}}{h} = \frac{680J}{1m} = 680N$；不计绳重、摩擦和水的阻力，由$W_{额外} = G_{动}h$可得，动滑轮的总重力$G_{动} = \frac{W_{额外}}{h} = \frac{W_{总} - W_{有用}}{h} = \frac{800J - 680J}{1m} = 120N$；由图乙可知，物体浸没在水中时，拉力$F_1 = 100N$，以物体和动滑轮的整体为研究对象，由力的平衡条件可得$4F_1 + F_{浮} = G + G_{动}$，则物体浸没在水中时受到的浮力$F_{浮} = G + G_{动} - 4F_1 = 680N + 120N - 4×100N = 400N$。（3）物体在水中匀速上升过程中对滑轮组的拉力$F_{拉} = nF_1 - G_{动} = 4×100N - 120N = 280N$，力的作用是相互的，所以滑轮组对物体的拉力等于$F_{拉}$，故物体在水中匀速上升过程中滑轮组的机械效率$η' = \frac{W'_{有用}}{W'_{总}}×100\% = \frac{F_{拉}h}{F_1s}×100\% = \frac{F_{拉}}{nF_1}×100\% = \frac{280N}{4×100N}×100\% = 70\%$。