《2025年亮点给力提优课时作业本九年级物理上册苏科版》

7. (2025·江苏苏州模拟)小明同学在中考体育考试中,选择了引体向上项目。如图是引体向上的示意图。小明同学在1分钟内做了8个规范的引体向上,则他在整个做引体向上过程中的功率最接近于 ()

A. 3W
B. 30W
C. 90W
D. 120W

答案： 解析:小明的质量约为50kg，重力约为500N，每次引体向上身体上升的高度约为0.4m,则小明每次引体向上所做的功$W = Gh = 500N×0.4m = 200J$，小明1分钟做的总功$W_{总} = 8W = 8×200J = 1600J$，则小明做功的平均功率$P = \frac{W_{总}}{t} = \frac{1600J}{60s} ≈ 27W$，最接近30W，故B正确。

8. 小华和妹妹一起坐双人秋千,当秋千从最高点摆到最低点的过程中,他们的重力做功的大小分别为$W_{1}$、$W_{2}$,重力做功的功率分别为$P_{1}$、$P_{2}$。若小华的体重比妹妹重,则下列说法正确的是 ()
A. $W_{1}= W_{2}$,$P_{1}= P_{2}$
B. $W_{1}\lt W_{2}$,$P_{1}＞P_{2}$
C. $W_{1}＞W_{2}$,$P_{1}＞P_{2}$
D. $W_{1}＞W_{2}$,$P_{1}= P_{2}$

答案： 解析:设小华和妹妹的重力分别为$G_1$、$G_2$，当秋千从最高点摆到最低点的过程中，他们下落的高度h相同，$G_1 ＞ G_2$，由$W = Gh$可知，小华和妹妹重力做功的大小关系为$W_1 ＞ W_2$；当秋千从最高点摆到最低点的过程中，他们下落的时间t相同，且$W_1 ＞ W_2$，由$P = \frac{W}{t}$可知，他们重力做功的功率大小关系为$P_1 ＞ P_2$。综上分析，C正确。

9. 某实验小组分别用如图所示的甲、乙两个滑轮组(每个滑轮等重),在相同时间内把同一重物提升相同高度。若$F_{1}和F_{2}$大小相等,不计绳重及摩擦,下列说法正确的是 ()

A. 力$F_{1}和F_{2}$做功的功率相同
B. 力$F_{1}和F_{2}$做的总功相同
C. 乙滑轮组更省力,两个滑轮组的机械效率一样高
D. 甲滑轮组的机械效率比乙滑轮组的机械效率高

答案： 解析:甲、乙两滑轮组中动滑轮上绳子的段数分别为$n_1 = 3$、$n_2 = 4$。设重物提升高度为h，绳子自由端移动的距离分别为$s_1 = 3h$、$s_2 = 4h$，则$s_1 ＜ s_2$，若$F_1$、$F_2$大小相等，由$W = Fs$可知，$W_1 ＜ W_2$，由于所用时间相同，由$P = \frac{W}{t}$可知，$P_1 ＜ P_2$，故A、B错误；已知$F_1 = F_2$，所以省力情况相同，故C错误；同一重物的重力相同，拉力$F_1 = F_2$，$n_1 ＜ n_2$，不计绳重和摩擦，由$η = \frac{W_{有用}}{W_{总}}×100\% = \frac{Gh}{Fs}×100\% = \frac{G}{nF}×100\%$可知，$η_1 ＞ η_2$，即甲滑轮组的机械效率比乙滑轮组的机械效率高，故D正确。

10. 一辆汽车沿直线通过两段平直路面,已知后一段路面比前一段路面更粗糙,汽车始终保持匀速。下列描述汽车行驶过程中发动机的功率$P随时间t$、克服阻力做功$W随运动路程s$变化的关系图像中,可能正确的是 ()

答案： 解析:由题意可知，汽车对路面的压力一定，后一段路面比前一段路面更粗糙，因此汽车在两段路面上受到的阻力的关系为$f_{前} ＜ f_{后}$。汽车始终保持匀速，处于平衡状态，由二力平衡条件可知，汽车在前后两段路面上发动机的牵引力均保持不变且等于摩擦力，则汽车在前后两段路面上发动机牵引力的关系为$F_{前} ＜ F_{后}$，汽车始终保持匀速，由$P = Fv$可知，前后两段路面上发动机功率保持不变且关系为$P_{前} ＜ P_{后}$，故A错误、B正确；由$W = Fs$可知，牵引力F不变时，牵引力做功与路程成正比，$F_{前} ＜ F_{后}$，由数学知识可知，汽车在前一段路面上克服阻力做功随路程的变化比在后一段路面上要慢，故C、D错误。

11. (2025·广东汕头期末)如图所示,轻质杠杆$OB可绕O$点转动,$OA= AB$,用细线将重物悬挂在$A$点,在$B点作用竖直向上的拉力F$,在保持杠杆水平静止的情况下 ()

A. 拉力$F$的大小为物重的2倍
B. 当悬挂点左移时,$F$将减小
C. 若$F$改为沿图中虚线方向施力,其力臂将增大
D. 若物重增加2N,$F$的大小增加1N

答案： 解析:由图可知，$OA = AB$，则阻力的力臂OA为动力力臂OB的一半，由杠杆的平衡条件可得$F×OB = G×OA$，则拉力$F = \frac{OA}{OB}×G = \frac{1}{2}G$，即拉力大小为物重的$\frac{1}{2}$，故A错误；当悬挂点左移时，动力臂、阻力不变，阻力臂变大，由杠杆的平衡条件可知，动力F将变大，故B错误；保持杠杆在水平位置平衡，将拉力F改为沿虚线方向施力，由力臂的定义可知，其力臂将减小，故C错误；若物重增加2N，由杠杆的平衡条件可得，F的增加量$ΔF = \frac{1}{2}ΔG = \frac{1}{2}×2N = 1N$，故D正确。

12. (2025·河北衡水期中)如图所示为建筑工地上常用的吊装工具,物体$M$是重5000N的配重,杠杆$AB的支点为O$,已知长度$OA:OB= 1:2$,滑轮下面挂有建筑材料$P$,每个滑轮重100N,工人体重为700N,杠杆与绳的自重、滑轮组摩擦均不计。当工人用300N的力竖直向下匀速拉动绳子时,建筑材料$P$以0.3m/s的速度上升。则 ()

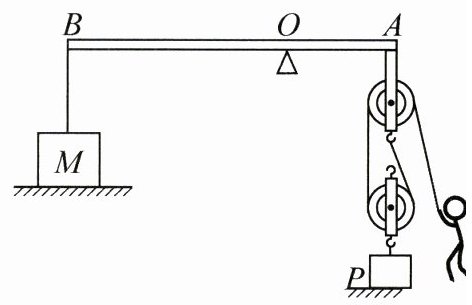
A. 滑轮组的机械效率为88.9%
B. 物体$M$对地面的压力为4500N
C. 工人对地面的压力为1000N
D. 工人拉绳的功率为270W

答案： 解析:由图可知动滑轮上绳子的段数$n = 2$，绳重及滑轮组摩擦均不计，由拉力$F = \frac{1}{n}(G + G_{动})$可得，建筑材料P的重力$G = nF - G_{动} = 2×300N - 100N = 500N$，滑轮组的机械效率$η = \frac{W_{有用}}{W_{总}}×100\% = \frac{Gh}{Fs}×100\% = \frac{Gh}{Fnh}×100\% = \frac{G}{nF}×100\% = \frac{500N}{2×300N}×100\% ≈ 83.3\%$，故A错误；定滑轮受向下的重力$G_{定}$、3段绳子向下的拉力3F、杠杆对定滑轮向上的拉力$F'_A$，由力的平衡条件可得$F'_A = 3F + G_{定} = 3×300N + 100N = 1000N$，杠杆对定滑轮的拉力和定滑轮对杠杆的拉力是一对相互作用力，大小相等，即$F_A = F'_A = 1000N$，由杠杆的平衡条件可得$F_A×OA = F_B×OB$，且$OA:OB = 1:2$，所以物体M对杠杆的拉力$F_B = \frac{OA}{OB}×F_A = \frac{1}{2}×1000N = 500N$，因为物体间力的作用是相互的，所以杠杆对物体M的拉力$F'_B = F_B = 500N$，物体M受竖直向下的重力、竖直向上的支持力和拉力，三力平衡，则物体M受到的支持力$F_{M支} = G_M - F'_B = 5000N - 500N = 4500N$，物体间力的作用是相互的，所以物体M对地面的压力$F_{M压} = F_{M支} = 4500N$，故B正确；当工人用300N的力竖直向下拉绳子时，由于力的作用是相互的，绳子对工人施加竖直向上的拉力$F' = F = 300N$，此时人受竖直向下的重力$G_{人}$、竖直向上的拉力$F'$和支持力$F_{支}$，由力的平衡条件可得$F' + F_{支} = G_{人}$，则$F_{支} = G_{人} - F' = 700N - 300N = 400N$，地面对人的支持力和人对地面的压力是一对相互作用力，所以工人对地面的压力$F_{压} = F_{支} = 400N$，故C错误；工人拉绳子的速度$v = nv_P = 2×0.3m/s = 0.6m/s$，则工人做功的功率$P = Fv = 300N×0.6m/s = 180W$，故D错误。