2025年周末小复习六年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年周末小复习六年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
9. 从一张长是102.8 cm的长方形纸卡上剪下两个圆和一个长方形(如图),正好可以做成一个圆柱,这个圆柱的体积是( )cm³。


答案:
题目中未提供该题答案
## 任务三 我会细心计算。(10分)
1. 计算下面立体图形的体积。

1. 计算下面立体图形的体积。

答案:
1.8×5×6 - 3.14×(2÷2)²×6 = 221.16(cm³)
2. 计算下面立体图形的体积。


答案:
2.$\frac{1}{2}$×3.14×(6÷2)²×(10 + 8) = 254.34(dm³)
## 任务四 我会解决问题。(47分)
### 主题情境:在艺术中发现数学
陶瓷制造和使用陶瓷的历史最早可追溯至新石器时代,千年匠心技艺,追求极致美学,才能够做成精美的作品。除了陶瓷,博山琉璃近日也备受关注,得到了很多人的喜爱。
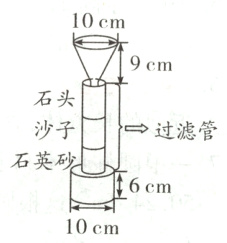
1. 徐林想制作一个污水过滤器进行污水过滤实验,就在他不知如何选材时,徐林的爸爸提出不妨用制作琉璃的材料试一试。如图是徐林绘制的模型图,将污水倒入上方的近似圆锥形的容器内,经过过滤管的过滤,清水可滴入下方的圆柱形容器中。(15分)
(1)这个圆锥形容器一次能装入多少毫升的污水? (7分)
(2)如果这些污水能全部过滤到下面的圆柱形容器中,水的高度是多少厘米? (不考虑过滤掉的杂质的体积)(8分)
### 主题情境:在艺术中发现数学
陶瓷制造和使用陶瓷的历史最早可追溯至新石器时代,千年匠心技艺,追求极致美学,才能够做成精美的作品。除了陶瓷,博山琉璃近日也备受关注,得到了很多人的喜爱。
1. 徐林想制作一个污水过滤器进行污水过滤实验,就在他不知如何选材时,徐林的爸爸提出不妨用制作琉璃的材料试一试。如图是徐林绘制的模型图,将污水倒入上方的近似圆锥形的容器内,经过过滤管的过滤,清水可滴入下方的圆柱形容器中。(15分)
(1)这个圆锥形容器一次能装入多少毫升的污水? (7分)
(2)如果这些污水能全部过滤到下面的圆柱形容器中,水的高度是多少厘米? (不考虑过滤掉的杂质的体积)(8分)

答案:
1.
(1)3.14×(10÷2)²×9×$\frac{1}{3}$ = 235.5(cm³)
235.5 cm³ = 235.5 mL
答:这个圆锥形容器一次能装入235.5 mL的污水。
(2)235.5÷3.14÷(10÷2)² = 3(cm)
答:水的高度是3 cm。
(1)3.14×(10÷2)²×9×$\frac{1}{3}$ = 235.5(cm³)
235.5 cm³ = 235.5 mL
答:这个圆锥形容器一次能装入235.5 mL的污水。
(2)235.5÷3.14÷(10÷2)² = 3(cm)
答:水的高度是3 cm。
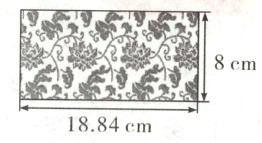
2. 李爷爷定制了一个圆柱形的陶瓷花瓶,要求工人师傅将一张画样按照3 : 1放大后临摹在花瓶的侧面(画样刚好完全覆盖了花瓶的侧面),下图是李爷爷选择的画样。(15分)
(1)这个花瓶的容积是多少毫升? (忽略花瓶厚度)(7分)
(2)如果工人每天可以为瓷瓶绘制150 cm²的图案,几天可以绘制完成? (8分)
(1)这个花瓶的容积是多少毫升? (忽略花瓶厚度)(7分)
(2)如果工人每天可以为瓷瓶绘制150 cm²的图案,几天可以绘制完成? (8分)

答案:
2.
(1)将一张画样按照3 : 1临摹在圆柱形瓷瓶侧面,所以瓷瓶的底面周长是18.84×3 = 56.52(cm),底面半径是56.52÷3.14÷2 = 9(cm),高是8×3 = 24(cm),容积是3.14×9²×24 = 6104.16(cm³)。
6104.16 cm³ = 6104.16 mL。
答:这个花瓶的容积是6104.16 mL。
(2)瓷瓶的侧面积是56.52×24 = 1356.48(cm²)
工人师傅绘制完瓷瓶侧面需要1356.48÷150 = 9.0432≈10(天)。
答:工人师傅绘制完成需要10天。
(1)将一张画样按照3 : 1临摹在圆柱形瓷瓶侧面,所以瓷瓶的底面周长是18.84×3 = 56.52(cm),底面半径是56.52÷3.14÷2 = 9(cm),高是8×3 = 24(cm),容积是3.14×9²×24 = 6104.16(cm³)。
6104.16 cm³ = 6104.16 mL。
答:这个花瓶的容积是6104.16 mL。
(2)瓷瓶的侧面积是56.52×24 = 1356.48(cm²)
工人师傅绘制完瓷瓶侧面需要1356.48÷150 = 9.0432≈10(天)。
答:工人师傅绘制完成需要10天。
3. 汝瓷是中国国家地理标志产品。制作汝瓷的手工艺人把一块棱长20 cm的正方体土坯揉捏、拍打,这块正方体土坯就变成了一块底面直径是20 cm的近似的圆锥形的泥土,乐乐算了一下这块圆锥形泥土的高度,计算过程如下。
乐乐列的算式:20×20×20÷[3.14×(20÷2)²]
乐乐列的算式对吗? 如果不对,请说出错误的原因。(7分)
乐乐列的算式:20×20×20÷[3.14×(20÷2)²]
乐乐列的算式对吗? 如果不对,请说出错误的原因。(7分)
答案:
3.不对,因为圆锥的体积公式为,所以,因此算式应该为20×20×20×3÷[3.14×(20÷2)²]。
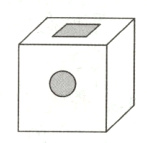
4. 下图是一个棱长为8 cm的正方体特种陶瓷元器件,在它的前后和上下两个底面的正中心位置分别挖去一个底面直径是2 cm的圆柱和一个底面是边长为2 cm的正方形的长方体。现在要给每个元器件表面镀一层金属材料,如果每平方米金属材料100元,工厂为1000个这种元器件镀金属材料需要多少钱? (10分)

答案:
4.圆柱形洞口的半径是2÷2 = 1(cm),
元器件的表面积 = 8×8×2 + (8×8 - 3.14×1²)×2 + (8×8 - 2×2)×2 + 2×8×2 + (2×8 - 3.14×1²)×2 + 3.14×1×2×(8 - 2) = 465.12(cm²) = 0.046512(m²),
每个元器件镀金属材料需要0.046512×100 = 4.6512(元),
1000个需要花费4.6512×1000 = 4651.2(元)。
答:1000个这种元器件镀金属材料需要4651.2元。
元器件的表面积 = 8×8×2 + (8×8 - 3.14×1²)×2 + (8×8 - 2×2)×2 + 2×8×2 + (2×8 - 3.14×1²)×2 + 3.14×1×2×(8 - 2) = 465.12(cm²) = 0.046512(m²),
每个元器件镀金属材料需要0.046512×100 = 4.6512(元),
1000个需要花费4.6512×1000 = 4651.2(元)。
答:1000个这种元器件镀金属材料需要4651.2元。
查看更多完整答案,请扫码查看


