《2025年周末小复习六年级数学下册人教版》

2. 子墨捏面团：把一块底面半径是3 cm，高是6 cm的圆柱形面团捏成一个底面周长是12.56 cm的圆锥。圆锥的高是多少厘米？(7分)

答案： $3.14×3^{2}×6 = 169.56(cm^{3})$
$12.56÷3.14÷2 = 2(cm)$
$169.56×3÷(3.14×2^{2}) = 40.5(cm)$
答：圆锥的高是40.5 cm。

3.(新题型)实验课上，老师让同学们测量一个底面半径是3 cm的圆锥形物体的高，实验室里没有提供直尺，聪明的田田做了如下实验：
①用天平称出物体的质量是20.8 g；
②向一个底面内直径是10 cm的圆柱形量杯里倒入水，水面高度是8 cm；
③将物体完全浸入量杯中，水面高度为8.6 cm，量杯里的水没有溢出。
(1)想一想，求这个圆锥形物体的高时，上面记录的信息中( )和( )是必须知道的。(填序号)(4分)
(2)请根据选出的信息，求出这个圆锥形物体的高。(7分)

答案：
(1)② ③
(2)$3.14×(10÷2)^{2}×(8.6 - 8)÷(\frac{1}{3}×3.14×3^{2}) = 5(cm)$
答：这个圆锥形物体的高是5 cm。

任务五 整理易错题
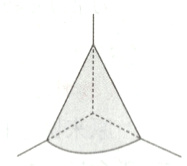
八、（作业易错题）学校进行维修，在一教室墙角堆放一堆沙子，已知沙堆底部弧长为3.14 m，沙堆的高为3 m，这个沙堆的体积是多少立方米？若每立方米沙子重2000 kg，则这堆沙子重多少吨？（8分）

答案： $3.14×4÷3.14÷2 = 2(m)$
$\frac{1}{3}×3.14×2^{2}×3×\frac{1}{4}=3.14(m^{3})$
$2000×3.14 = 6280(kg)$ 6280 kg = 6.28 t
答：这个沙堆的体积是3.14 $m^{3}$，这堆沙子重6.28 t。

九、（名师补充易错题）3D电脑动画成像技术展示活动中，技术人员用一个直角边是10 cm的等腰直角三角形，绕着一条直角边所在直线旋转成一个圆锥；又用一个边长是10 cm的正方形，绕着正方形的一条对称轴旋转成一个圆柱。（12分）
1. 形成的圆锥和圆柱的体积各是多少？（除不尽的得数保留两位小数）（8分）
2. 圆锥和圆柱的体积相比，哪个大？大多少？（4分）

答案： 1. 圆锥的体积：
$\frac{1}{3}×3.14×10^{2}×10≈1046.67(cm^{3})$
圆柱的体积：$3.14×(10÷2)^{2}×10 = 785(cm^{3})$
答：形成的圆锥的体积是1046.67 $cm^{3}$，圆柱的体积是785 $cm^{3}$。
2. 1046.67 ＞ 785 1046.67 - 785 = 261.67($cm^{3}$)
答：圆锥的体积大，大261.67 $cm^{3}$。