《2025年木头马分层课课练小学数学三年级下册人教版浙江专版》

（1）李阿姨做了长方形薄饼，不小心将一块薄饼撕成了两部分(如图)，这两部分的( )。

A. 周长和面积都相等
B. 周长相等，面积不相等
C. 面积相等，周长不相等
D. 周长和面积都不相等

答案：
(1) B

（2）一块地砖的面积是 25 平方分米，40 块地砖的面积是( )平方米。
A. 1 B. 10 C. 100 D. 1000

答案：
(2) B

（3）下面 4 个图形的周长都是 16 厘米，面积最大的图形是( )。
A. 2 厘米
B. 4 厘米
C. 7 厘米
D. 3 厘米

答案：
(3) B 解析 周长相同的长方形和正方形，正方形的面积最大。

2. 分别计算下面两个图形的周长和面积。(单位：厘米)

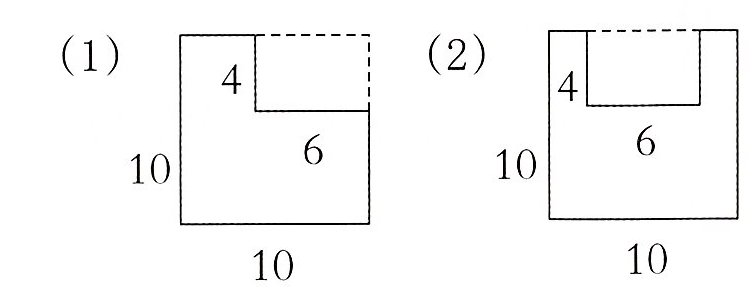
答案：
(1) 周长：10×4 = 40(厘米) 面积：10×10 - 6×4 = 76(平方厘米)
(2) 周长：10×4 + 4×2 = 48(厘米) 面积：10×10 - 6×4 = 76(平方厘米) 解析 两小题图中的面积都一样，都是10×10 - 6×4 = 76(平方厘米)。图
(1)中的周长等于正方形的周长，是10×4 = 40(厘米)，图
(2)中的周长等于正方形的周长加上2条4厘米的线段，是40 + 4×2 = 48(厘米)。

3. (新情境·地域建筑)嵊泗革命烈士纪念碑坐落在舟山泗礁本岛菜园镇，基座长 100 分米，宽 7 米，占地面积是多少平方米？

答案： 100分米 = 10米 10×7 = 70(平方米) 解析 先统一单位，将100分米换算成10米，再计算面积，列式为10×7 = 70(平方米)。

4. 把一张长 12 分米、宽 8 分米的长方形彩纸，剪成边长是 4 厘米的小正方形纸片，一共能剪多少个？

答案： 12分米 = 120厘米 8分米 = 80厘米 120÷4 = 30(个) 80÷4 = 20(个) 30×20 = 600(个) 解析 12分米 = 120厘米，8分米 = 80厘米，沿长方形的长能剪出120÷4 = 30(个)4厘米，沿长方形的宽能剪出80÷4 = 20(个)4厘米，所以一共可以剪出30×20 = 600(个)边长为4厘米的小正方形。

5. 下图是由两个正方形拼成的长方形。已知长方形的周长是 48 厘米，那么长方形的面积是多少平方厘米？

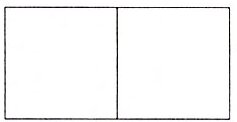
答案： 宽：48÷2÷(1 + 2)=8(厘米) 长：8×2 = 16(厘米) 面积：16×8 = 128(平方厘米) 解析 观察图形可知，长方形的宽就是正方形的边长，长方形的长是宽的2倍。长方形一条长和一条宽的和是48÷2 = 24(厘米)，也就是长方形的宽的(1 + 2)倍，所以宽是24÷(1 + 2)=8(厘米)，长是8×2 = 16(厘米)，面积是16×8 = 128(平方厘米)。

6. 用 56 米长的栅栏围成长 20 米的长方形，其中一边利用围墙，怎样围才能使围成的长方形面积最大？最大的面积是多少平方米？

答案： ①长边靠墙： 宽：(56 - 20)÷2 = 18(米) 面积：20×18 = 360(平方米) ②宽边靠墙： 宽：56 - 20×2 = 16(米) 面积：20×16 = 320(平方米) 360＞320 长边靠墙时面积最大，最大的面积是360平方米。 解析 长方形有2种情况，一种情况是长边靠墙，那56米是两条宽和一条长的长度，所以宽是(56 - 20)÷2 = 18(米)，面积是20×18 = 360(平方米)；另一种情况是宽边靠墙，那么56米是一条宽和两条长的长度，所以宽是56 - 20×2 = 16(米)，面积是20×16 = 320(平方米)。360＞320，长边靠墙时面积最大，最大的面积是360平方米。