【题目】在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),直线
为参数),直线![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系
(1)求曲线C与直线l的极坐标方程;
(2)若直线l与曲线C相交,交点为![]() ,直线与x轴交于Q点,求
,直线与x轴交于Q点,求![]() 的取值范围.
的取值范围.
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 点,射线
点,射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
【题目】甲、乙二人进行一次象棋比赛,每局胜者得1分,负者得0分(无平局),约定一方得4分时就获得本次比赛的胜利并且比赛结束,设在每局比赛中,甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立,已知前3局中,甲得1分,乙得2分.
,各局比赛结果相互独立,已知前3局中,甲得1分,乙得2分.
(1)求甲获得这次比赛胜利的概率;
(2)设![]() 表示从第4局开始到比赛结束所进行的局数,求
表示从第4局开始到比赛结束所进行的局数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】《九章算术》是我国古代著名数学经典,其中对勾股定理的论述,比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小;以锯锯之,深一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺,问这块圆柱形木料的直径是多少?长为0.5丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).己知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,
寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,![]() )
)
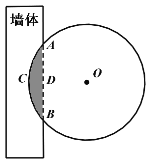
A.300立方寸B.305.6立方寸C.310立方寸D.316.6立方寸
【题目】“地摊经济”是李克强总理在本届政府工作报告中向全国人民发出的口号,某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 |
| 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() ,
,![]() ,
,
(1)试求![]() ,若变量
,若变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求恰好2个都是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求恰好2个都是“好数据”的概率.
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为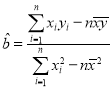 ,
,![]() )
)
【题目】如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900

(1)求证:PC⊥BC
(2)求点A到平面PBC的距离
【题目】在直角坐标![]() 中,圆
中,圆![]() ,圆
,圆![]() 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求圆![]() 的公共弦的参数方程。
的公共弦的参数方程。

