【题目】设函数，，

（1）求曲线过原点的切线方程；

（2）设，若函数的导函数存在两个不同的零点，，求实数的范围：

（3）在（2）的条件下证明：

（1）若某顾客购物消费1800元，作为网络平台的商家，通过返现的期望进行判断，是希望顾客直接选择返回180元现金，还是选择参加3次答题返现？

（2）若某顾客购物消费7200元并且都选择参加答题返现，请计算该顾客答对多少次概率最大，最有可能返回多少现金？

【题目】如图，矩形和菱形所在的平面相互垂直，，，，.

（1）求证：平面；

（2）求二面角的正切值.

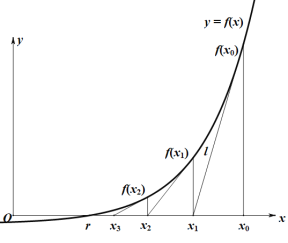
【题目】牛顿迭代法（Newtonsmethod）又称牛顿-拉夫逊方法（Newton-Raphsonmethod），是牛顿在17世纪提出的一种近似求方程根的方法.如图，设是的根，选取作为初始近似值，过点作曲线的切线，与轴的交点的横坐标，称是的一次近似值，过点作曲线的切线，则该切线与轴的交点的横坐标为，称是的二次近似值.重复以上过程，得到的近似值序列.请你写出的次近似值与的次近似值的关系式______，若，取作为的初始近似值，试求的一个根的三次近似值______（请用分数做答）.

A.0.99%B.99%C.49.5%.D.36.5%

【题目】我们可从这个商标中抽象出一个如图靠背而坐的两条优美的曲线，下列函数中大致可“完美”局部表达这对曲线的函数是（ ）

A.B.

C.D.

【题目】如图，三棱锥中，底面△是边长为2的正三角形，，底面，点分别为，的中点.

（1）求证：平面平面；

（2）在线段上是否存在点，使得三棱锥体积为？若存在，确定点的位置；若不存在，请说明理由.

【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系，随机调查了某中学高三某班名学生每周课下钻研数学时间(单位：小时)与高三下学期期中考试数学解答题得分，数据如下表：

（1）根据上述数据，求出数学考试中的解答题得分与该学生课下钻研数学时间的线性回归方程，并预测某学生每周课下钻研数学时间为小时其数学考试中的解答题得分；

（2）从这人中任选人，求人中至少有人课下钻研数学时间不低于小时的概率.

参考公式：，其中， ；参考数据：

【题目】已知椭圆的离心率为，且以原点为圆心，以短轴长为直径的圆过点.

（1）求椭圆的标准方程；

（2）若过点的直线与椭圆交于不同的两点，且与圆没有公共点，设为椭圆上一点，满足（为坐标原点），求实数的取值范围.

【题目】“克拉茨猜想”又称“猜想”，是德国数学家洛萨克拉茨在年世界数学家大会上公布的一个猜想：任给一个正整数，如果是偶数，就将它减半；如果为奇数就将它乘加，不断重复这样的运算，经过有限步后，最终都能够得到，得到即终止运算，己知正整数经过次运算后得到，则的值为（ ）

A.或B.或C.D.或或