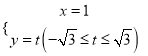【题目】在直角坐标中，圆，圆。

(Ⅰ)在以O为极点，x轴正半轴为极轴的极坐标系中，分别写出圆的极坐标方程，并求出圆的交点坐标(用极坐标表示)；

(Ⅱ)求圆的公共弦的参数方程。

【答案】（1）（2）,.

【解析】试题分析：（1）利用进行互化即可；（2）由两圆的公共点求出公共弦的普通方程，再利用直线的点与倾斜角得到参数方程．

解题思路:曲线的普通方程、参数方程、极坐标方程的互化，往往要利用或合理选参进行求解．

试题解析：（1）根据公式：

圆C1、 C2的极坐标方程分别为： ，

联立： 解得：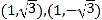

∴圆C1与圆C2的交点极坐标分别为：

（2）把（1）中两圆交点极坐标化为直角坐标，

得：

∴此两圆公共弦的普通方程为：

∴此弦所在直线过（1，0）点，倾斜角为90°

∴所求两圆的公共弦的参数方程为：

关闭