在直角坐标系xOy中，直线l1的参数方程为（t为参数），直线l2的参数方程为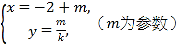.设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．

（1）写出C的普通方程；

（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ(cosθ+sinθ) =0，M为l3与C的交点，求M的极径.

【题目】众所周知的“太极图”，其形状如对称的阴阳两鱼互抱在一起，因此被称为“阴阳鱼太极图”．如图是放在平面直角坐标系中的“太极图”的一个示意图，整个图形是一个圆面，其中黑色区域在轴右侧部分的边界为一个半圆．给出以下命题：

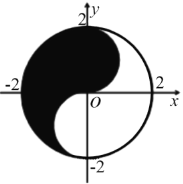
①在太极图中随机取一点，此点取自黑色部分的概率是；

②当时，直线与白色部分有公共点；

③黑色阴影部分中一点，则的最大值为2；

④设点，点在此太极图上，使得，的范围是．

其中所有正确结论的序号是（ ）

A.①②B.②③C.①③D.①④

【题目】某中学从甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班学生成绩的众数是83，乙班学生成绩的平均数是86，则的值为（ ）

A.7B.8C.9D.10

【题目】已知函数.

（1）若且，求的单调区间；

（2）若在处取得最大值，求实数的取值范围.

【题目】如图1，在四边形中，，，，.把沿着翻折至的位置，构成三棱锥如图2.

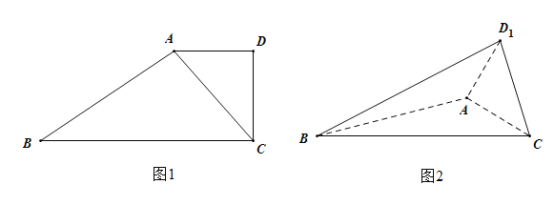
（1）当时，证明：；

（2）当三棱锥的体积最大时，求点到平面的距离.

【题目】年初，新冠病毒引发的肺炎疫情在全球肆虐，为了有效地控制病毒的传播，某医院组织专家统计了该地区名患者新冠病毒潜伏期的相关信息，数据经过汇总整理得到如下图所示的频率分布直方图（用频率作为概率）.潜伏期不高于平均数的患者，称为“短潜伏者”，潜伏期高于平均数的患者，称为“长潜伏者”.

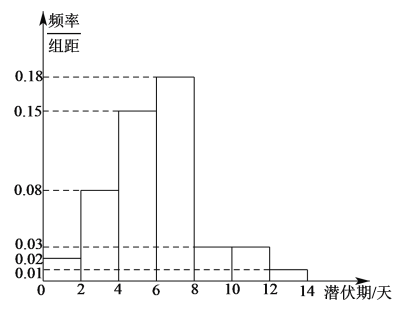
（1）求这名患者潜伏期的平均数（同一组中的数据用该组区间的中点值作代表）和众数；

（2）为研究潜伏期与患者年龄的关系，得到如下列联表，请将列联表补充完整，并根据列联表判断是否有的把握认为潜伏期长短与患者年龄有关；

（3）研究发现，某药物对新冠病毒有一定的抑制作用，需要从这人中分层选取位岁以下的患者做Ⅰ期临床试验，再从选取的人中随机抽取两人做Ⅱ期临床试验，求两人中恰有人为“短潜伏者”的概率.

附表及公式：

.

【题目】在平面直角坐标系xOy中，直线C1的参数方程为（t为参数，0＜α＜π），曲线C2的参数方程为（φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系.

（1）求曲线C2的极坐标方程；

（2）设曲线C1与曲线C2的交点分别为A，B，M（﹣2，0），求|MA|2+|MB|2的最大值及此时直线C1的倾斜角.

【题目】正方体棱长为，点为边的中点，动点在正方体表面上运动，并且总保持，则动点的轨迹的周长为（ ）

A.B.C.D.

A.15.5尺B.12.5尺C.9.5尺D.6.5尺

【题目】我校甲、乙、丙三名语文老师和、、三名数学老师被派往某县城一中和二中支教，其中有一名语文老师和一名数学老师被派到了一中，其它老师都去二中支教，则甲与被派到同一所学校的概率为（ ）

A.B.C.D.