【题目】已知

（1）当时，求的最大值；

（2）若存在使，得关于的方程有三个不相同的实数根，求实数的取值范围.

【题目】如图，过抛物线焦点的直线交抛物线于，两点，记以，为直径端点的圆为圆.

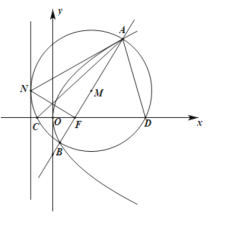
（1）证明：圆与抛物线的准线相切；

（2）设，点在焦点的右侧，圆与轴交于，两点，记和的面积为，求的最大值（其中，点为圆与抛物线准线的切点）

【题目】面积为2的中，，分别是，的中点，点在直线EF上，则的最小值是（ ）

A.B.C.D.

【题目】已知函数.

（1）讨论的单调性；

（2）若函数在点处的切线的斜率为，证明：当时，.

【题目】如图，在三棱柱中，平面，为的中点，交于点，，.

（1）证明：平面；

（2）若，求二面角的余弦值.

（Ⅰ）求B；

（Ⅱ）若b=2，求△ABC面积的最大值.

A. （0，）B. （，e）C. （，）D. （0，）

（1）求曲线C1和曲线C2的直角坐标方程；

（2）若点P是曲线C1上一动点，过点P作线段OP的垂线交曲线C2于点Q，求线段PQ长度的最小值．

【题目】中国古代的四书是指：《大学》、《中庸》、《论语》、《孟子》，甲、乙、丙、丁名同学从中各选一书进行研读，已知四人选取的书恰好互不相同，且甲没有选《中庸》，乙和丙都没有选《论语》，则名同学所有可能的选择有______种.

观察散点图，两个变量不具有线性相关关系，现考虑用函数对两个变量的关系进行拟合.参考数据（其中）：

（1）求y关于x的回归方程，并求y关于u的相关系数（精确到0.01）.

（2）该产品采取订单生产模式（根据订单数量进行生产，即产品全部售出）.根据市场调研数据，若该产品单价定为80元，则签订9千件订单的概率为0.7，签订10千件订单的概率为0.3；若单价定为70元，则签订10千件订单的概率为0.3，签订11千件订单的概率为0.7.已知每件产品的原料成本为30元，根据（1）的结果，要想获得更高利润，产品单价应选择80元还是70元，请说明理由.

参考公式：对于一组数据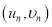，，…，，其回归直线的斜率和截距的最小二乘估计分别为：，，相关系数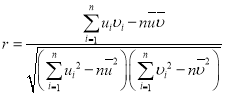.